Processing math: 100%

5. 位相反転

元の時間領域アナログサイン波の初期位相が ϕ [rad] である時、ϕ±π [rad] の初期位相を持つ時間領域アナログサイン波は「位相が反転している」と言い、元のサイン波のグラフを上下反転したグラフとなります。

式で表せば、元の時間領域アナログサイン波の式が

f(t)=a⋅sin(w⋅t+ϕ)

ならば、位相が反転しているサイン波の式は

f′(t)=a⋅sin{w⋅t+(ϕ±π)}

となります。
ここで

f′(t)=a⋅sin{w⋅t+(ϕ±π)}=a⋅sin{(w⋅t+ϕ)±π}=−a⋅sin(w⋅t+ϕ)

なので

位相を反転する = 振幅の符号を反転する

とも言えます。

例えば次の図 1 は振幅が a=1、角周波数が w=2π、初期位相が ϕ=0 の時間領域アナログサイン波です。

図1: 元のサイン波

f(t)=1⋅sin(2π⋅t)

このサイン波の位相を反転させると次の図2のグラフとなります。

図2: 図1のサイン波の位相を反転

f′(t)=1⋅sin(2π⋅t±π)=−1⋅sin(2π⋅t)

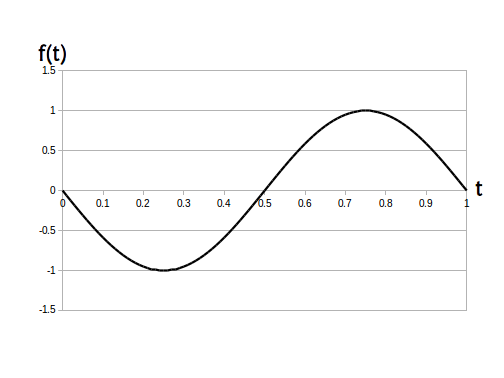
なお、元のサイン波と位相反転したサイン波を足し合わせると f(t)=0 となります。
この性質はイヤホンのノイズキャンセリング機能などに応用されています。