時間領域ディジタル信号 $f[i]$ が与えられた時に、その信号が周期的な信号であるのか、それともただのノイズなのかは自己相関関数(autocorrelation function) $\textrm{R}[n]$ を使って判定できます。
ただし前提として $f[i]$ が(弱)定常過程であるとします。 そこでまずここでは定常過程について説明します。
定常過程とは $f[i]$ がある確率に従って出力されている時に、$f[i]$ の平均
\[ \textrm{E} \left ( f[i] \right ) \]が時刻 $i$ によらず定数になり、かつ $n$ を遅延時刻とした時に $f[i]$ と $f[i+n]$ の共分散
\[ Cov \left ( f[i], f[i+n] \right ) \]が時刻 $i$ によらず遅延時刻 $n$ のみで値が決まる信号列のことです。
なお共分散の性質より
\[ Cov \left ( f[i], f[i+n] \right ) = Cov \left ( f[i+n], f[i] \right ) \]
という等式が成り立ちます。
また定常過程の場合は時刻 $i$ が関係無くなるので
という等式も成り立ちます。
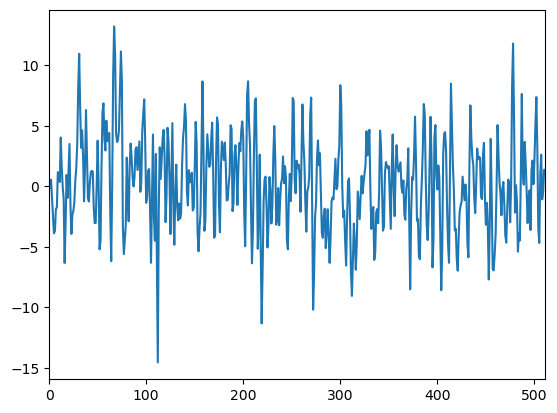
では具体的に定常過程となっている信号の例を示しましょう。
以下の図 1 は信号
を $i=0$ から $i=511$ まで 512 点出力したグラフで、いわゆる「移動平均(MA)モデル」と呼ばれるモデルです(図1〜4のソースはこちら)。
ここで $e[i]$ は各時刻毎に独立な平均 0、分散 1 の正規乱数です。
確率で変動しますので、サンプリングするたびにグラフの形が変わることに注意して下さい。

一見するとただのノイズの様に見えますが、平均と共分散を計算すると
平均 : ※ 導出はこのページの下の方を参照
\[ \textrm{E}(f[i]) = 0 \]共分散 : ※ 導出はこのページの下の方を参照
\[ Cov \left ( f[i], f[i+0] \right ) = 14 \] \[ Cov \left ( f[i], f[i+1] \right ) = 9 \] \[ Cov \left ( f[i], f[i+2] \right ) = 2 \] \[ Cov \left ( f[i], f[i+n] \right ) = 0 \ , \ (n \geq 3) \]
の様に平均が定数になり、共分散も $i$ が含まれておらず $n$ だけで値が決まっているので、$f[i]$ は定常過程であることが分かります。
この共分散をグラフで表すと図2の通りになります。
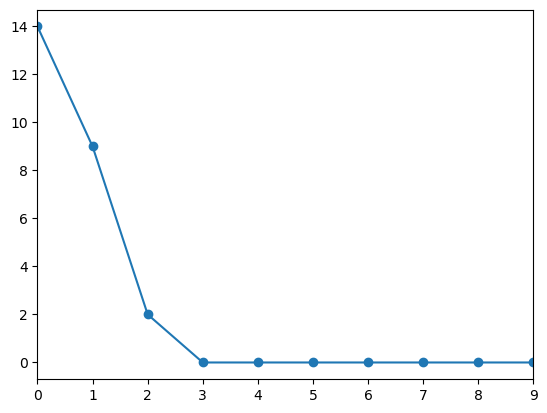
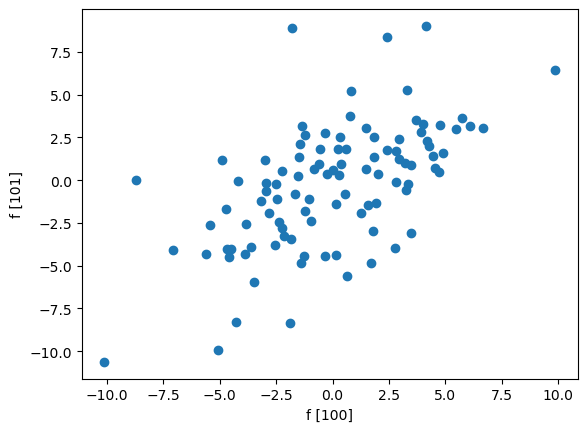
図 2 を見ると、n=0 以外では n=1 の時の共分散が最も大きいので i = 100, n = 1 とし、信号を 100 回サンプリングして f[100] と f[101] 間の散布図を作ったのが図 3 です。
※ i = 0 でなくて、i = 100 からサンプリングしているのは初期変動の影響を取り除くためです。
確かに f[100] と f[101] の平均は 0 で、強い正の相関があることが分かります。
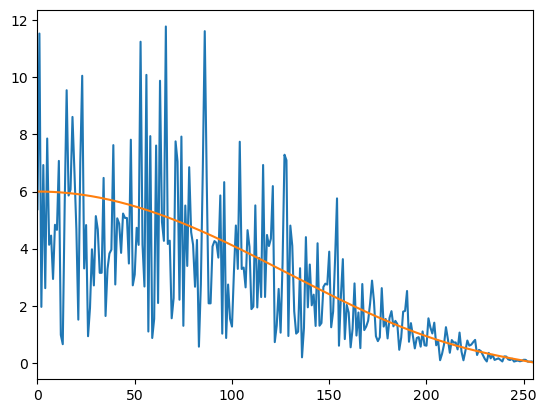
参考までに図1の信号の振幅スペクトルを図4に示します。
※ 橙色の線は理論的なスペクトル包絡線
もう少し複雑な例として図 5 を見て下さい。
図 5 の信号も図1と同様に移動平均(MA)モデルから生成した信号で、具体的には平均0、分散1の正規乱数列をバンドパスフィルタに通して生成しています(図5〜8のソースはこちら)。
こちらも確率で変動しますので、サンプリングするたびにグラフの形が変わることに注意して下さい。
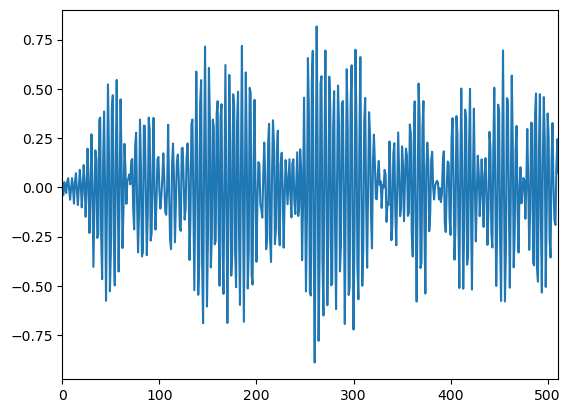
一見すると平均が上下していて定常過程でないような印象を受けますが、もちろんこの信号も定常過程になっています。
平均が 0 なのは簡単に分かりますが、共分散は計算すると図 6 の様になります。
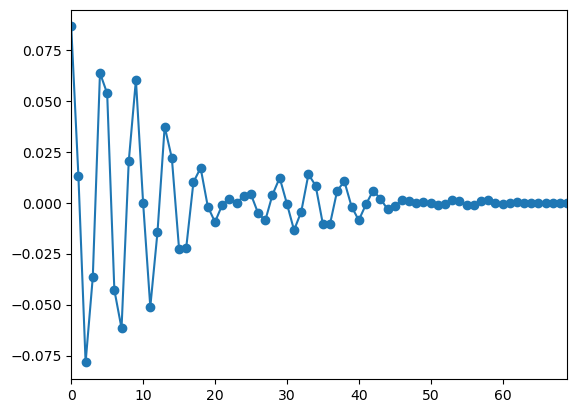
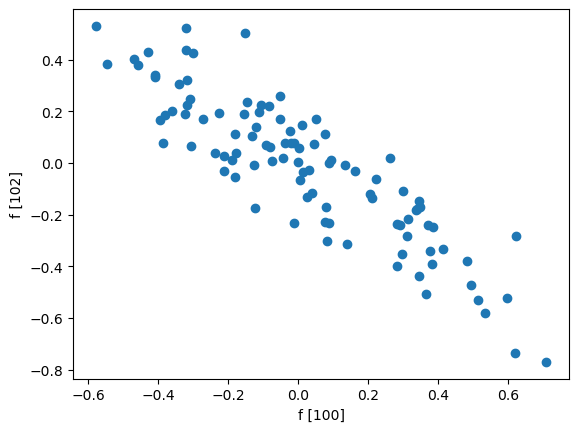
図 6 を見ると、n=0 以外では n=2 の時の共分散が(絶対値を取ると)最も大きいので i = 100, n = 2 とし、信号を 100 回サンプリングして f[100] と f[102] 間の散布図を作ったのが図 7 です。
確かに f[100] と f[102] の平均は 0 で、強い負の相関があることが分かります。
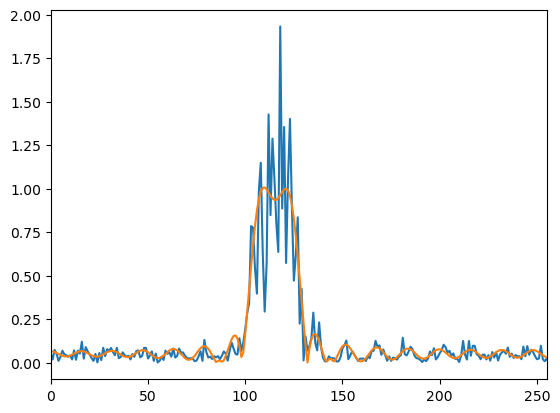
参考までに図5の信号の振幅スペクトルを図8に示します。
※ 橙色の線は理論的なスペクトル包絡線
ここで $e[i]$ は各時刻毎に独立な平均 $\mu = 0$、分散 $\sigma^2 = 1$ の正規乱数とする。
平均は以下の様にして求められる。
\begin{align*} \textrm{E}(f[i]) &= \textrm{E}( e[i] + 3 \cdot e[i-1] + 2 \cdot e[i-2] ) \\[5pt] &= \textrm{E} ( e[i] ) + 3 \cdot \textrm{E} ( e[i-1] ) + 2 \cdot \textrm{E} ( e[i-2] ) \\[5pt] &= 0 \end{align*}共分散は以下の様にして求められる。
\begin{align*} Cov \left ( f[i], f[i+n] \right ) &= \textrm{E} \left \{ \left( f[i] - \textrm{E}(f[i]) \right ) \cdot \left( f[i+n] - \textrm{E}(f[i+n]) \right ) \right \} \\[5pt] &= \textrm{E} \left \{ \left( e[i] + 3 \cdot e[i-1] + 2 \cdot e[i-2] \right ) \cdot \left( e[i+n] + 3 \cdot e[i+n-1] + 2 \cdot e[i+n-2] \right ) \right \} \\[5pt] &= 1 \cdot \textrm{E} \left( e[i] \cdot e[i+n] ) \right ) + 3 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+n] \right ) + 2 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+n] \right ) \\[5pt] &+ 3 \cdot \textrm{E} \left( e[i] \cdot e[i+n-1] ) \right ) + 9 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+n-1] \right ) + 6 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+n-1] \right ) \\[5pt] &+ 2 \cdot \textrm{E} \left( e[i] \cdot e[i+n-2] ) \right ) + 6 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+n-2] \right ) + 4 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+n-2] \right ) \\[5pt] \end{align*}ここで $i$ と $j$ を 0 以上の任意の整数とした時
\begin{align*} \textrm{E}( e[i] \cdot e[j] ) &= \textrm{E} \left \{ (e[i] - \mu)\cdot(e[j]-\mu) +\mu\cdot e[i] + \mu \cdot e[j] - \mu^2 \right \} \\[5pt] &= \textrm{E} \left \{ (e[i] - \mu)\cdot(e[j]-\mu) \right \} + \mu^2 \end{align*}となるので、 $i = j$ の時は
\[ \textrm{E}( e[i] \cdot e[j] ) = \sigma^2 + \mu^2 = 1 \]$i \neq j$ の時は各時刻毎に独立であることから
\[ \textrm{E}( e[i] \cdot e[j] ) = 0 \]となる。
よって$n=0$ の時
\begin{align*} Cov \left ( f[i], f[i] \right ) &= 1 \cdot \textrm{E} \left( e[i] \cdot e[i] ) \right ) + 3 \cdot \textrm{E} \left ( e[i-1] \cdot e[i] \right ) + 2 \cdot \textrm{E} \left ( e[i-2] \cdot e[i] \right ) \\[5pt] &+ 3 \cdot \textrm{E} \left( e[i] \cdot e[i-1] ) \right ) + 9 \cdot \textrm{E} \left ( e[i-1] \cdot e[i-1] \right ) + 6 \cdot \textrm{E} \left ( e[i-2] \cdot e[i-1] \right ) \\[5pt] &+ 2 \cdot \textrm{E} \left( e[i] \cdot e[i-2] ) \right ) + 6 \cdot \textrm{E} \left ( e[i-1] \cdot e[i-2] \right ) + 4 \cdot \textrm{E} \left ( e[i-2] \cdot e[i-2] \right ) \\[5pt] &= 1 + 9 + 4\\[5pt] &= 14 \end{align*}$n=1$ の時
\begin{align*} Cov \left ( f[i], f[i+1] \right ) &= 1 \cdot \textrm{E} \left( e[i] \cdot e[i+1] ) \right ) + 3 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+1] \right ) + 2 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+1] \right ) \\[5pt] &+ 3 \cdot \textrm{E} \left( e[i] \cdot e[i] ) \right ) + 9 \cdot \textrm{E} \left ( e[i-1] \cdot e[i] \right ) + 6 \cdot \textrm{E} \left ( e[i-2] \cdot e[i] \right ) \\[5pt] &+ 2 \cdot \textrm{E} \left( e[i] \cdot e[i-1] ) \right ) + 6 \cdot \textrm{E} \left ( e[i-1] \cdot e[i-1] \right ) + 4 \cdot \textrm{E} \left ( e[i-2] \cdot e[i-1] \right ) \\[5pt] &= 3 + 6 \\[5pt] &= 9 \end{align*}$n=2$ の時
\begin{align*} Cov \left ( f[i], f[i+2] \right ) &= 1 \cdot \textrm{E} \left( e[i] \cdot e[i+2] ) \right ) + 3 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+2] \right ) + 2 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+2] \right ) \\[5pt] &+ 3 \cdot \textrm{E} \left( e[i] \cdot e[i+1] ) \right ) + 9 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+1] \right ) + 6 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+1] \right ) \\[5pt] &+ 2 \cdot \textrm{E} \left( e[i] \cdot e[i] ) \right ) + 6 \cdot \textrm{E} \left ( e[i-1] \cdot e[i] \right ) + 4 \cdot \textrm{E} \left ( e[i-2] \cdot e[i] \right ) \\[5pt] &= 2 \end{align*}$n=3$ の時
\begin{align*} Cov \left ( f[i], f[i+3] \right ) &= 1 \cdot \textrm{E} \left( e[i] \cdot e[i+3] ) \right ) + 3 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+3] \right ) + 2 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+3] \right ) \\[5pt] &+ 3 \cdot \textrm{E} \left( e[i] \cdot e[i+2] ) \right ) + 9 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+2] \right ) + 6 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+2] \right ) \\[5pt] &+ 2 \cdot \textrm{E} \left( e[i] \cdot e[i+1] ) \right ) + 6 \cdot \textrm{E} \left ( e[i-1] \cdot e[i+1] \right ) + 4 \cdot \textrm{E} \left ( e[i-2] \cdot e[i+1] \right ) \\[5pt] &= 0 \end{align*}同様にして $n \geq 4$ の時も 0