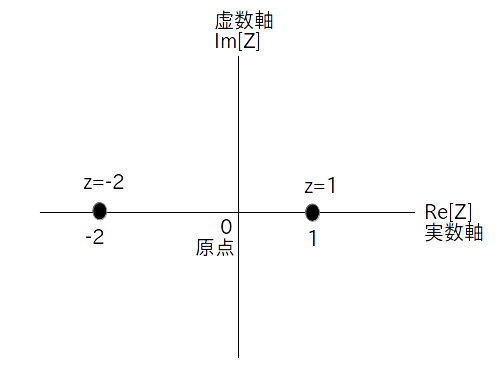(例) $x = -2, \ 0, \ 1.5$ の位置
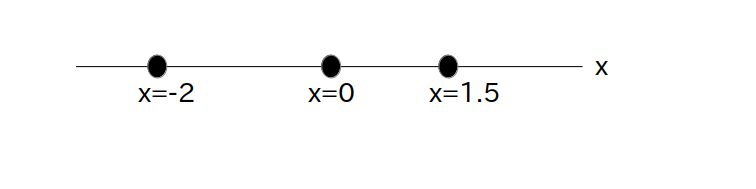
複素数をきちんと理解するためには「複素平面(complex plane)」または「ガウス平面」についても学ぶ必要があります。
まず実数とは何か思い出してみましょう。
実数は「実数直線」と呼ばれる $-\infty$ から $\infty$ まで続く直線の上のある点のことでした(図1)。
(例) $x = -2, \ 0, \ 1.5$ の位置
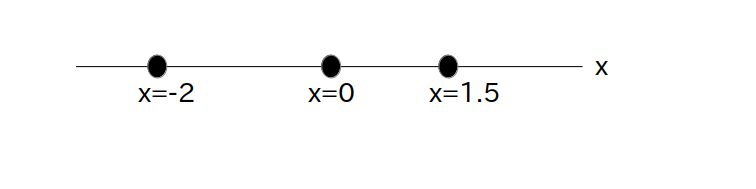
一方複素数 $z$ には実数を表す実部 Re[z] の他に虚数を表す虚部 Im[z] がありましたので、複素数を実数直線上の一点として考えることは出来ません。
ではどうするかというと実数直線に対して、原点で直角に交わる軸(虚数を表す軸)を一つ加えて複素平面という平面を作ります。
そして複素数はその複素平面上の点あるいはベクトルとみなします(図2)。
例:
$z = 1 + 2 \cdot j$
及び
$z = -2 - j$
の位置は以下の図で示した場所になる

図2において、実数を表す横軸を「実数軸」(または実軸)、虚数を表す縦軸を「虚数軸」(または虚軸)と言います。
また複素数 $z$ がベクトルであることを強調したい場合は、図2の様に $z$ の位置を表す点に向かって原点から矢印を引きます。
この矢印の長さが複素数の絶対値を表しています。
さて複素数は実数直線を拡張して作った複素平面上の点ですので、当然ながら実数も複素数のひとつです。
実際のところ虚部が 0 の複素数、つまり実数軸上にある複素数のことを実数と呼んでいます(図3)。
例:
$z = 1$
及び
$z = -2$
の位置は以下の図で示した場所になる