ここでは掛け算の特殊な場合である回転について説明します。


(1) 回転

絶対値が 1 の複素数の掛け算は回転を表します。

回転

$\theta$ [rad] を任意の実数値としたとき、絶対値が 1 の複素数

\[ \textrm{e}^{\{j\cdot \theta\}} \]

を考える。
これを任意の複素数 $z$ に掛けると

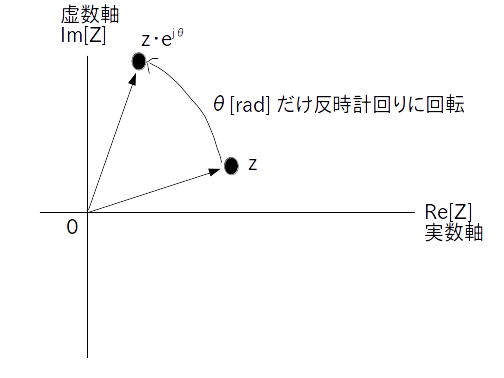
\[ z \cdot \textrm{e}^{\{j\cdot \theta\}} = \left [ |z| \cdot \textrm{e}^{ \{ j\cdot \angle \ z \} } \right ] \cdot \textrm{e}^{\{ j \cdot \theta\} } = |z| \cdot \textrm{e}^{\{j\cdot (\angle \ z+\theta)\}} \]

が得られるが、これは原点を中心として $z$ が $\theta$ [rad] だけ複素平面内で反時計回りに回転したことを意味する。
なお $\theta$ がマイナスの時は時計回りに回転する。

上の式の意味は図で考えた方が分かりやすいでしょう
図1を見れば元の複素数が $\theta$ [rad] だけ逆時計回りに回転移動していることが一目瞭然です。

図1: 回転

　


(2) -1 を掛ける

さらに回転の特別の場合として複素数に -1 を掛けた時のことを考えます。

結論から言うと複素数 $z$ は 180 度回転します。

-1 を掛けると180度回転 \[ -1 = \textrm{e}^{j\pi} \]

より

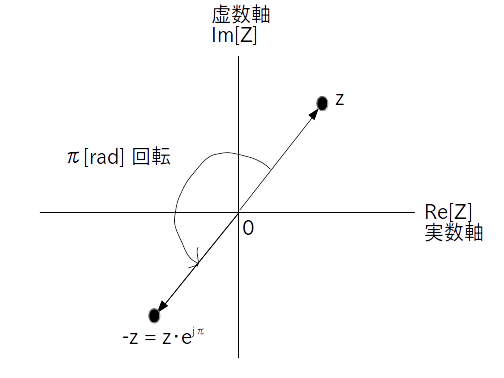
\[ -z = z \cdot \textrm{e}^{j\pi} = |z| \cdot \textrm{e}^{\{j\cdot (\angle \ z + \pi)\}} \]

なので、複素数 $z$ に -1 を掛けることは $z$ を複素平面内で180度回転させることと同じ意味である。

これも図で見ると理解しやすいです(図2)。

図2: -1 をかけると180度回転

　


(補足) 回転行列との関係

複素数の回転は回転行列を使った 2 次元ベクトルの回転と実質的に同じであることを説明します。

まず任意の 2 次元ベクトル $(x,y)$ を元に複素数

\[ z = x + y \cdot j \]

を作ります。
$z$ を $\theta$ だけ回転させた複素数は上で示した通りに

\[ |z| \cdot \textrm{e}^{\{j\cdot (\angle \ z+\theta)\}} \]

となります。
次にこれを直交形式に変換して sin と cos を加法定理を使って展開します。

\begin{align*} |z| \cdot \textrm{e}^{\{j\cdot (\angle \ z+\theta) \}} = & (|z| \cdot \cos (\angle \ z+\theta)) + \{ |z| \cdot \sin (\angle \ z+\theta) \} \cdot j \\[10pt] (\text{加法定理より}) = & \left \{ |z| \cdot \cos \angle \ z \cdot \cos\theta - |z| \cdot \sin \angle \ z \cdot \sin\theta \right \} \\ & + \left \{ |z| \cdot \sin \angle \ z \cdot \cos\theta + |z| \cdot \cos \angle \ z \cdot \sin\theta \right \} \cdot j \\[10pt] =& \left \{ x \cdot \cos\theta - y \cdot \sin\theta \right \} + \left \{ y \cdot \cos\theta + x \cdot \sin\theta \right \} \cdot j\\ \end{align*}

さてこの結果の実部を $x'$、虚部を$y'$とすると

\[ x' = x \cdot \cos \theta - y \cdot \sin \theta \] \[ y' = y \cdot \cos \theta + x \cdot \sin \theta \]

となりますが、これを行列演算で書き直すと次の様になります。

\[ \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} \]

これは回転行列を使って 2次元ベクトル $(x,y)$ を $\theta$ [rad] だけ回転させて 2次元ベクトル $(x',y')$ を求めていることを意味します。