次は「フィードバック機構」について説明します。
フィードバック機構は出力信号 $y[i]$ が伝達関数 $\textrm{H}_1(z)$ を持つフィルタ(インパルス応答は $h_1[i]$)に通されてから入力信号 $x[i]$ に再加算されるフィルタのことで、畳込み演算で表すと
\[ y[i] = x[i] + \sum_{n=0}^{\infty} \left \{ h_1[n] \cdot y[i-n] \} \right \} \]という出力をするフィルタです。
上式の両辺をZ変換すると
\[ Y(z) = X(z) + \textrm{H}_1(z) \cdot Y(z) \]になりますので、フィードバック機構の伝達関数は
\[ \textrm{H}(z) = \frac{Y(z)}{X(Z)} = \frac{1}{1-\textrm{H}_1(z)} \]
となります。
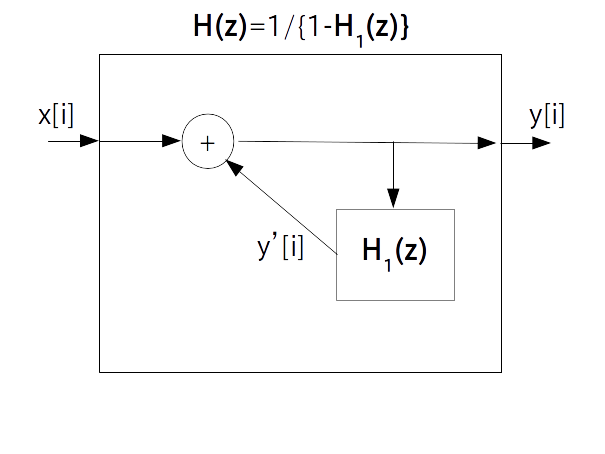
またフィードバック機構のブロック図は次の様になります。
