「サンプリング」とはアナログ時間領域信号 $f(t)$ の値をある間隔ごとに飛び飛びに取り出してディジタル時間領域信号 $f[i]$ に変換する処理のことで「標本化」とも言います。
「サンプリング」も「標本化」も良く使われる単語なのでどちらか好きな方を使って良いです。
では実際にサンプリングについて説明する前に、いくつか事前に覚えておいて欲しい用語と公式を挙げておきます。
・ サンプリング周波数 $f_s$ ・・・ アナログ信号 $f(t)$ に対して $1$ 秒間に何回サンプリングするかを表す正の整数値、単位は Hz(ヘルツ)
・ サンプリング角周波数 $w_s$ ・・・ $f_s$ を角周波数に変換した値、単位は rad/秒(ラジアン毎秒)
・$w_s = 2\pi\cdot f_s$ の関係がある
・ サンプリング間隔 $\tau$ (タウ) ・・・ $f(t)$ に対して何秒おきにサンプリングするかを表す正の実数値、単位は 秒
・ $\tau = 1/f_s = 2\pi/w_s$ の関係がある
※ サンプリング間隔は等間隔で無くても良いのですが今回は等間隔でサンプリングすることにします
例えば $f_s = 10$ [Hz] だとすると $f(t)$ の値を $1$ 秒間に $10$ 回サンプリングして取り出す事を意味しますので、その間隔は $\tau = 1/10 = 0.1$ [秒]ということになります。
では、これを踏まえてサンプリングの仕方をステップに分けて説明していきます。
そもそも時間領域アナログ信号 $f(t)$ が無いと始まらないので、まずサンプリング対象の $f(t)$ を選びます。
次にサンプリング周波数 $f_s$ [Hz]を決めます。
この値はユーザがシステム要件等から自分で決める必要があり、大きくしても小さくしてもそれぞれメリット・デメリットがあります。
なお $f_s$ [Hz]を決めたらサンプリング間隔 $\tau$ [秒]は公式 $\tau = 1/f_s$ から自動的に決まります。
次に時刻 $i$ の範囲、つまりディジタル信号 $f[i]$ の値域を決めます。
$i$ は負の時刻から始まっても良いのですが、今回は話を簡単にするために 0 から始めることにします。
さて $i$ は整数値としたので、$i=0,1,2,\cdots$ の様に時刻 $i=0$ からサンプリングを開始し、最大時刻 $i_{\textrm{MAX}}$ までサンプリングを終えたら停止します。
ここで $i_{\textrm{MAX}}$ の値は何秒間サンプリングするかによって決まります。
$1$ 秒間に $f_s$ 回サンプリングしますので、 $\textrm{T}_s$ 秒間サンプリングするとしたら $i_{\textrm{MAX}} = f_s \cdot \textrm{T}_s$ になります。
ただし $f_s \cdot \textrm{T}_s$ が整数値でない時は、その値を超える最小の整数値を $i$ の最大値 $i_{\textrm{MAX}}$ にすることに今回はします。
例えば $f_s = 10$で $\textrm{T}_s = 1.55$ なら $f_s \cdot \textrm{T}_s = 15.5$ なので $i_{\textrm{MAX}} = 16$ となります。
$i$の範囲を決めたら、後は
\begin{align*} f[i] = f( \tau \cdot i ) \ , \ (i=0,1,\cdots、i_{\textrm{MAX}}) \end{align*}と $\tau$ 秒おきに $f(t)$ の値を $f[i]$ に代入していくだけです。
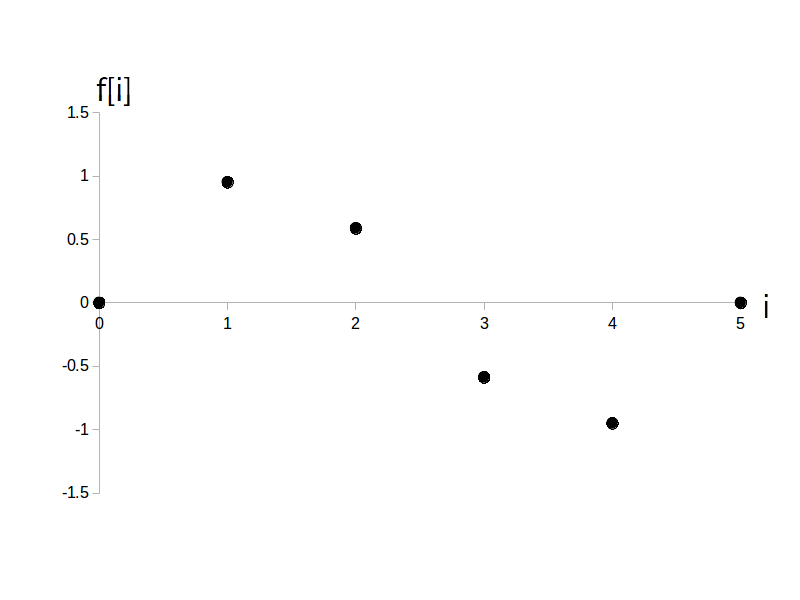
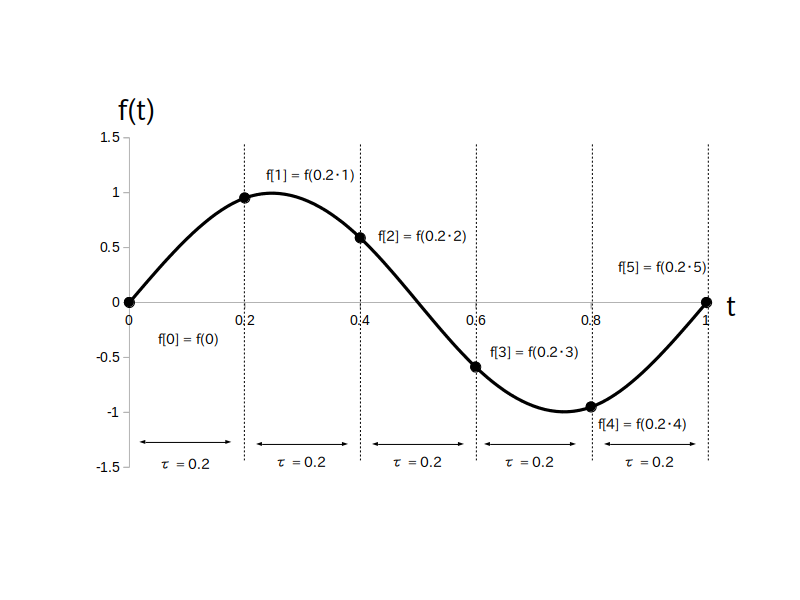
例えば図1は $f(t) = \sin( 2\pi \cdot t )$ を $f_s = 5$ [Hz]、$\tau = 0.2$ [秒] で $\textrm{T}_s = 1$ 秒間サンプリングしている状況です。
$\tau = 0.2$ [秒]おきに $f[i]$ の値が取り出されている事に注目して下さい。
$i_{\textrm{MAX}} = f_s \cdot \textrm{T}_s = 5$ なので、$i$ の範囲は $i = \{0,1,2,3,4,5\}$ となります。

サンプリングの結果として図2の様な時間領域ディジタル信号が得られます。