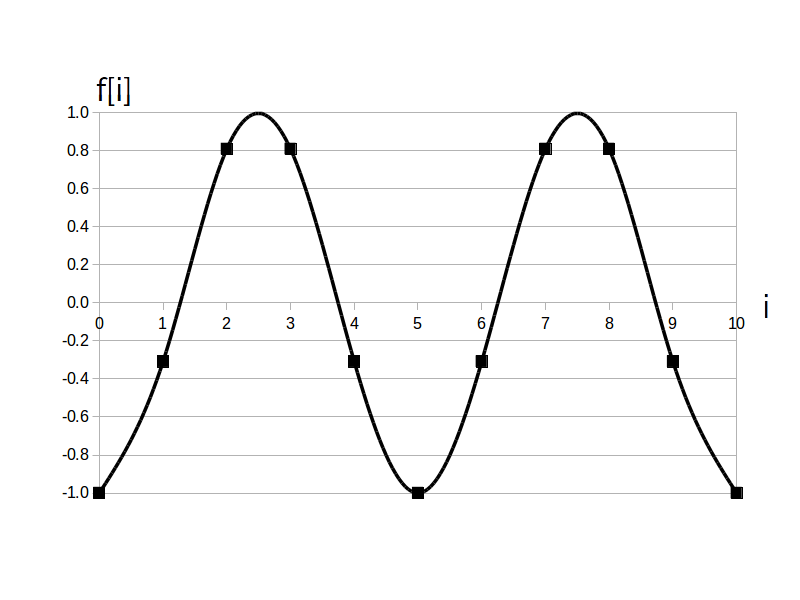
$f[i] = 1 \cdot \sin( 2\pi /5 \cdot i -\pi/2 ) \ , \ (i=0,1, \cdots, 10)$
時間領域ディジタル信号の一種である時間領域ディジタルサイン波にも秒の概念はありませんので、周波数という概念は本来はありません。
よって角周波数という概念も本来はありません。
その代わり1ページ目で示したように周期 $\textrm{T}_d$ を使って時間領域ディジタルサイン波は定義されます。
周期 $\textrm{T}_d$ は、 $i$ が何点進めば波が 1 回振動するのかを表す数字です。
この $\textrm{T}_d$ の値を変えるとグラフでは横方向の伸縮が変わります。
$\textrm{T}_d$ が大きいとグラフは横方向で伸びます。逆に小さいと横方向で縮みます。
なお$\textrm{T}_d$ は実数でも構いませんが、特に整数の場合はきれいにアップダウンするようなグラフになります。
例えば1ページ目で例示したサイン波(下に再掲)は $\textrm{T}_d = 5$ [点]なので、 $i$ が $5$ 点進む毎に 1 回サイン波がアップダウンしていることが分かります。
$f[i] = 1 \cdot \sin( 2\pi /5 \cdot i -\pi/2 ) \ , \ (i=0,1, \cdots, 10)$

ところで、時間領域ディジタルサイン波には周波数や角周波数という概念は無いと上では言いましたが、実際には周波数または角周波数を便宜上にでも考慮した方が色々都合の良い時が多いです。
そこで、「角周波数 $w$ [rad/秒] の時間領域アナログサイン波 $f(t)$ をサンプリング周波数 $f_s$ [Hz] でサンプリングして時間領域ディジタルサイン波 $f[i]$ を求めた」という状況を仮定し、サンプリング元のアナログサイン波 $f(t)$ の角周波数 $w$ [rad/秒]、または周波数 $f$ [Hz] をディジタルサイン波 $f[i]$ の(角)周波数とみなすことにします。
さて、アナログサイン波を $f_s$ [Hz] でサンプリングした場合、$1$ 点サンプリングする毎にサンプリング間隔 $\tau = 1/f_s$ [秒]だけ間隔が空きます。
つまり周期 $\textrm{T}_d$ [点]の分だけ信号値をサンプリングするには $\textrm{T}_d \cdot \tau $ [秒]必要です。
このことから、次のように時間領域ディジタルサイン波の角周波数や周波数が定義できます。
サンプリング周波数 $f_s$ [Hz] と周期 $\textrm{T}_d$ [点]を使って時間領域ディジタルサイン波の周波数と角周波数を定義する
ここで
サンプリング間隔 ・・・ $\tau = 1/f_s$ [秒]
周期 $\textrm{T}_d$ [点] サンプリングするのに必要な時間(つまり秒に換算した周期) ・・・ $\textrm{T} = \textrm{T}_d \cdot \tau$ [秒]
なので
時間領域ディジタルサイン波の(便宜上の)周波数・・・ $f = \frac{1}{\textrm{T}} = \frac{1}{\textrm{T}_d \cdot \tau} = \frac{f_s}{\textrm{T}_d}$ [Hz]
時間領域ディジタルサイン波の(便宜上の)角周波数 ・・・ $w = 2\pi \cdot f = 2 \pi \cdot \frac{f_s}{\textrm{T}_d}$ [rad/秒]
なお、最後の公式を変形すると
\[ \textrm{T}_d = 2 \pi \cdot \frac{f_s}{w} \]となりますので角周波数 $w$ [rad/秒] とサンプリング周波数 $f_s$ [Hz]を使って時間領域ディジタルサイン波の定義を書きなおすことも出来ます。
または
\[ f[i] = a \cdot \cos \left ( \frac{w}{f_s} \cdot i + \phi \right ) \]