スペクトル $\textrm{F}(w)$ のグラフのことを「スペクトル図」と呼びます。
スペクトル $\textrm{F}(w)$ は複素関数なので、普通にスペクトル図を描くと角周波数軸、実軸、虚軸の3つの軸を持つ3次元グラフになります。
ただし3次元グラフは分かりにくいので、「振幅スペクトル(またはパワースペクトル)図」と「位相スペクトル図」の2つのグラフに分けて表すことが多いです。
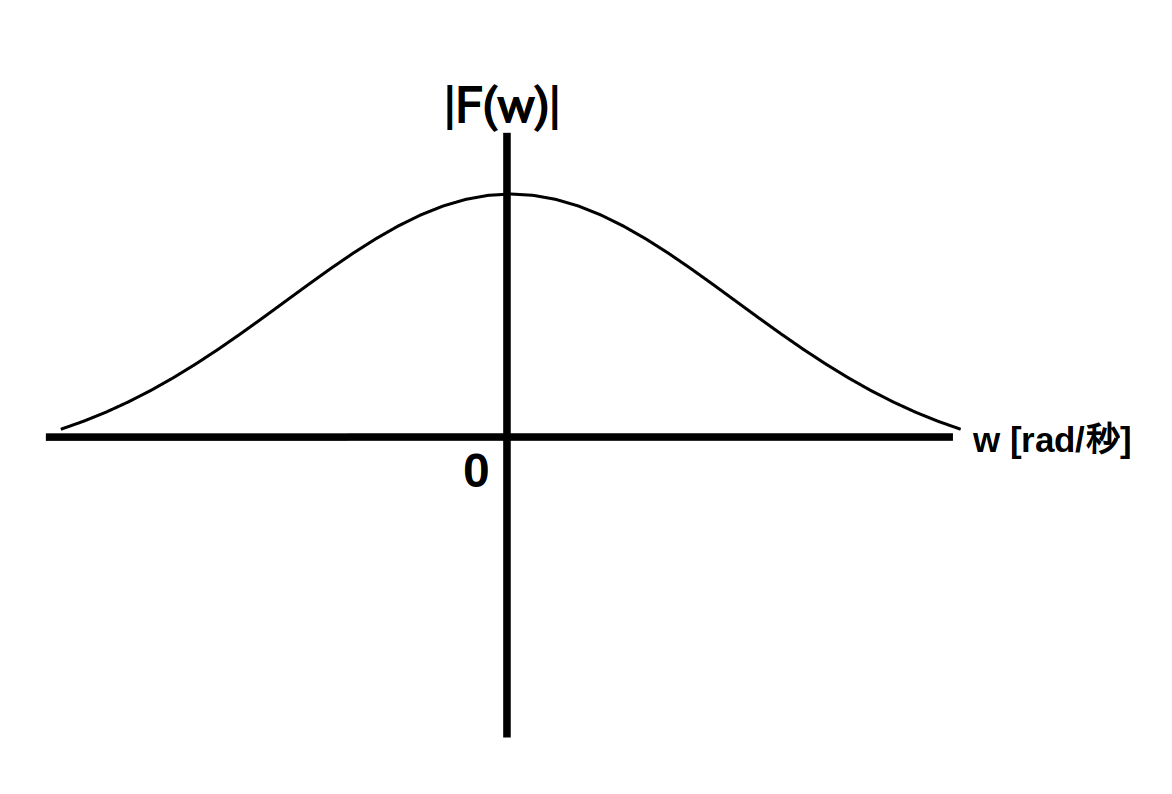
さて、振幅スペクトル図は横軸を角周波数 $w$ [rad/秒]、縦軸を振幅スペクトル $|\textrm{F}(w)|$ とするグラフです。
例を図1に示します。

パワースペクトル図は振幅スペクトル図を縦方向に自乗するだけなので省略します。
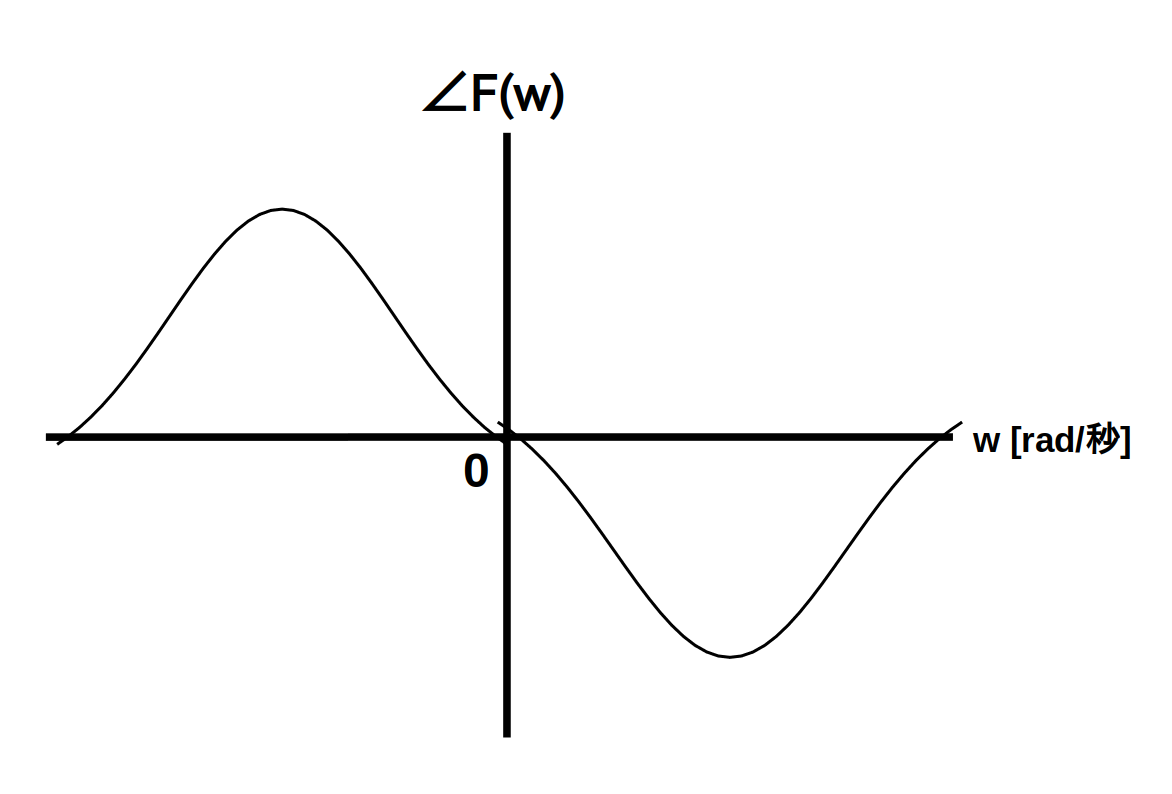
一方、位相スペクトル図は横軸を角周波数 $w$ [rad/秒]、縦軸を位相スペクトル $\angle\textrm{F}(w)$ とするグラフです。
例を図2に示します。