Z変換の例としてまずは有限長の時間領域ディジタル信号から考えてみます。
まず 時刻 $i < 0$ で $f[i]=0$ とします(つまり片側 Z 変換を考えます)。
さらに有限の正整数 $\textrm{L}$ に対して $f[0]$から$f[\textrm{L}-1]$まで値が入っていて、残りは全て $f[i]=0, (i=\textrm{L},\textrm{L}+1,\cdots)$ である時間領域ディジタル信号が与えられたとします。
つまり
というディジタル信号を考えます。
このとき $i$ が $\textrm{L}$ を超えると $f[i]$ は全て $0$ となるので、(片側) Z 変換は以下の式の様に簡単に求まります。
\begin{align*} \textrm{F}(z) & = \sum_{i=0}^\infty \{ f[i] \cdot z^{-i} \} \\ & = \sum_{i=0}^{\textrm{L}-1} \{ f[i] \cdot z^{-i} \} \\ & = f[0] + \frac{f[1]}{z} + \frac{f[2]}{z^2} + \cdots + \frac{f[\textrm{L}-1]}{z^{\textrm{L}-1}} \end{align*}
逆変換も簡単に求まります。
もし $\textrm{F}(z)$ が
の形で与えられている時、逆変換は有限長の時間領域ディジタル信号 $f[0], f[1], f[2], \cdots, f[\textrm{L}-1]$ になります。
また収束領域は次の様になります。 とりあえず $z=0$ をZ変換に代入してみると
\begin{align*} \textrm{F}(0) = f[0] + \frac{f[1]}{0} + \frac{f[2]}{0} + \cdots + \frac{f[\textrm{L}-1]}{0} \rightarrow \infty \end{align*}
となるので $\textrm{F}(0)$ は発散します。
一方 $z=0$ 以外の値を代入しても発散しません。
つまり
「収束領域は原点 $z=0$ を除く Z 平面全域」
となります。
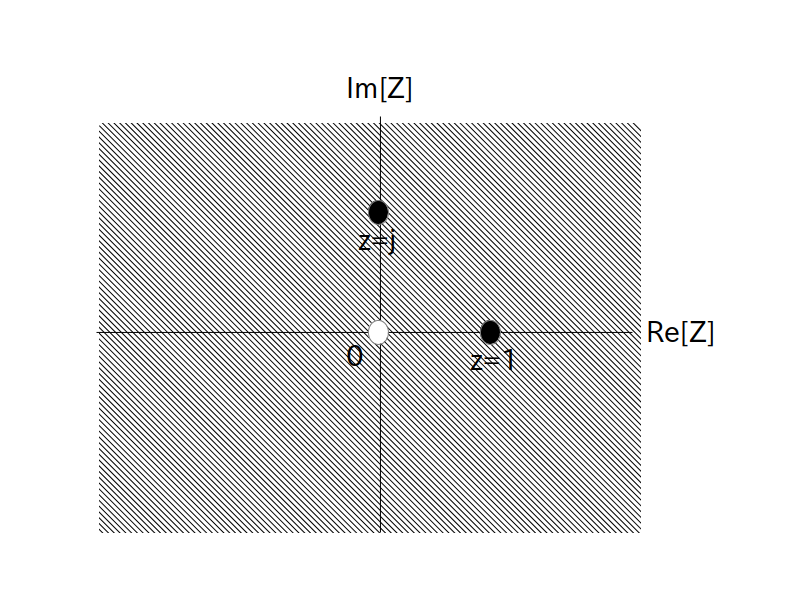
この収束領域を図で表すと以下の図1となります。
図1の原点 $z=0$ を除く斜め線で表した領域が収束領域です。

では例として $\textrm{L} = 4$、 $f[i] = \{ 1, 2, 3, 4, 0, 0, \cdots \}$ のZ変換
\[ \textrm{F}(z) = 1 + \frac{2}{z} + \frac{3}{z^2} + \frac{4}{z^3} \]
に対して図 1 に示した $z=1$ を代入してみましょう。
図1を見る限り $z=1$ は収束領域に含まれていますので、$\textrm{F}(z)$ の式にそのまま $z=1$ の値を代入して
が求める答となります。
同様に次は $z=j$ を代入してみましょう。
図1を見る限り $z=j$ も収束領域に含まれていますので、$\textrm{F}(z)$ の式にそのまま $z=j$ の値を代入して
が求める答となります。
ある $0$ 以上の正整数 $n$ に対し、
\begin{align*} f[i] = \begin{cases} 1 & (i=n) \\ 0 & (i \neq n) \end{cases} \end{align*}
である信号のことを「ディジタルインパルス信号」といって記号 $\delta[i-n]$ で表します。
ここではこの $\delta[i-n]$ の Z 変換を求めてみましょう。
ただし $n$ が 0 かどうかで結果が変わりますので、とりあえず $n=0$ の場合、つまり $\delta[i]$ の Z 変換を考えます。
$\delta[i]$は時刻 $i=0$ の時だけ 1 で、それ以外は 0 という信号ですので Z 変換は以下の式になります。
\begin{align*} \textrm{F}(z) &= \sum_{i=-\infty}^{\infty} \{ f[i] \cdot z^{-i} \} \\ &= \cdots + 0 \cdot z^2 + 0 \cdot z^1 + 1 \cdot z^0 + 0 \cdot z^{-1} + 0 \cdot z^{-2} + \cdots \\ &= 1 \end{align*}逆変換も簡単で、もしZ変換が
\[ \textrm{F}(z) = 1 \]の形で与えられているなら逆変換は $\delta[i]$ になります。
また今回はどの様な $z$ の値を代入しても必ず $\textrm{F}(z) = 1$ となりますので
「収束領域は Z 平面全域」
になります。
では試しに $z=1$ と $z=j$ の $\textrm{F}(z)$ の値を求めてみましょう。
当然どちらも収束して
となるだけです。
次にディジタルインパルス信号 $\delta[i-n]$ が $n \ne 0$ の場合を考えます。
$\delta[i-n]$ は $i=n$ の時だけ $1$ で、それ以外は $0$という信号ですのでZ変換は以下の式になります。
\begin{align*} \textrm{F}(z) &= \sum_{i=-\infty}^{\infty} \{ f[i] \cdot z^{-i} \} \\ & = \cdots + 0 \cdot z^{-(n-1)} + 1 \cdot z^{-n} + 0 \cdot z^{-(n+1)} + \cdots \\ & = z^{-n} \end{align*}逆変換も簡単で、もしZ変換が
\[ \textrm{F}(z) = z^{-n} \]の形で与えられている時、逆変換は $\delta[i-n]$ になります。
また例1と同様に $z=0$ 以外の時は収束しますので
「収束領域は$z=0$ を除くZ平面全域」
となります。
では試しに $n=2$ 、つまり
\[ \textrm{F}(z) = z^{-2} \]
に対して $z=1$ を代入してみましょう。
$z=1$ は上で示した図1を見ると収束領域内に含まれていますので $\textrm{F}(z)$ にそのまま $z=1$ を代入して
が得られます。
同様に $z=j$ も代入してみましょう。
$z=j$ も収束領域内に含まれていますので $\textrm{F}(z)$ にそのまま $z=j$ を代入して
が得られます。
次は実数 $a (\neq 0) $ に対する等比数列
\[ f[i] = a^i = \{ 1, a, a^2, \cdots \} \]
の Z 変換を求めてみましょう。
ただし $i \geq 0$ とします(つまり片側 Z 変換を使います)。
まず $f[i]$ を片側 Z 変換の定義にそのまま代入して $\textrm{F}(z)$ を求めます。
\begin{align*} \textrm{F}(z) = \sum_{i=0}^\infty \{ a^i \cdot z^{-i} \} = \sum_{i=0}^\infty \{ a \cdot z^{-1} \}^i \end{align*}次は以下の無限等比級数の和の収束公式を利用して収束後の式に変形します。
初項 $\beta$、公比 $r$ としたとき、$|r| < 1$ならば
\[ \sum_{i=0}^\infty \beta \cdot r^i \rightarrow \frac{\beta}{1-r} \]今回は初項 $\beta = 1$、公比 $r = a \cdot z^{-1}$ なので、もし $|a \cdot z^{-1}| < 1$ つまり $|z| > |a|$ ならば
\begin{align*} \textrm{F}(z) = \frac{1}{1-a \cdot z^{-1}} \end{align*}となります。
逆変換も簡単で、もし Z 変換が
\[ \textrm{F}(z) = \frac{1}{1-a \cdot z^{-1}} \]の形で与えられているなら逆変換は $f[i] = a^i$ となります。
また、和の収束公式の収束条件より
収束領域は $|z| > |a|$
となります。
この収束領域を図で表したのが以下の図2で、図中の半径 $|a|$ の円の「外側」が収束領域になります。
※ 半径 $|a|$ の円上の点は収束領域では無いので注意して下さい。
半径 $|a|$ の円の「外側」が収束領域
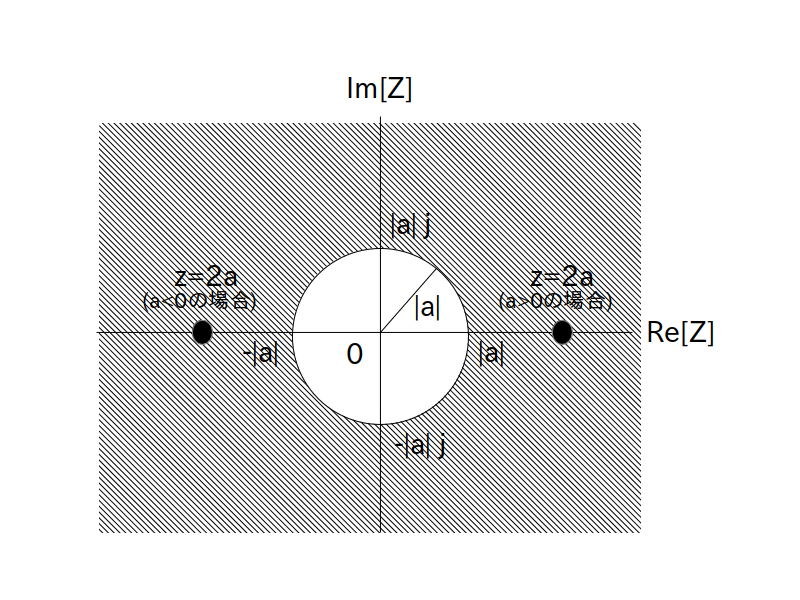
では試しに $z=2a$ をZ変換に代入してみましょう。
図2を見る限り $z=2a$ は収束領域に含まれています($a$の符号により位置が変わります)ので、$\textrm{F}(z)$ にそのまま $z=2a$ の値を代入して
\begin{align*} \textrm{F}(2a) = \frac{1}{1-\frac{a}{2a}} = \frac{1}{1-\frac{1}{2}} = 2 \end{align*}となります。
なお円上もしくは内側にある $z$ を代入した場合は級数が収束しませんので「発散する」が答となります。