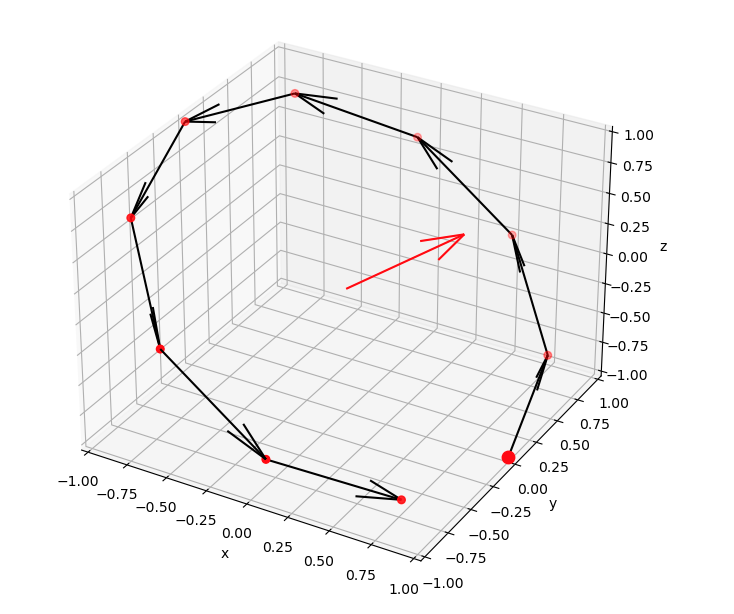
赤い矢印 : 回転軸 $u$
大きい赤い丸 : 初期位置 $v$
小さい赤い丸 : 回転後の位置
複素数に絶対値が 1 の複素数を掛ける事は実質上2 次元ベクトルの回転を表していました。
同様にクォータニオンに絶対値が 1 のクォータニオンを掛ける事も 4 次元ベクトルの回転を表します。
ところで 3 次元空間は 4 次元空間の部分空間とみなせるので、うまくクォータニオンを決めてあげれば 3 次元ベクトルも回転できるはずです。
そこでここではクォータニオンを使った 3 次元ベクトルの回転について考えてみましょう。
まず回転させたい 3 次元ベクトルを $v = (x,y,z)$ とします。
$v$ のままだとクォータニオンの演算が出来ないので、$v$ を実部が 0 であるクォータニオンの虚部とみなして
というクォータニオン $V$ を作ります。
すると $V$ は実部が 0 である 3 次元部分空間上のベクトルになるので、実質的には $V$ も 3 次元ベクトルとみなすことが出来ます。
次に
\[ q = (w_q, v_q ) \]
を絶対値が 1 の任意のクォータニオンとします。
では早速 $q$ を $V$ に掛けてみて $V$ が回転するか確認してみましょう。
右と左のどちらから $q$ を掛けるかという問題がありますがとりあえず左から掛けてみます。
ハミルトン積を使って $qV$ の実部と虚部を計算すると以下の様になります。
ここで「$\cdot$」は内積で「$\times$」はクロス積です。
実部 :
\[ {\mathrm Re}[ qV ] = -v_q \cdot v \]虚部 :
\[ {\mathrm Im}[ qV ] = w_q v + v_q \times v \]
すると $v_q$ か $v$ がゼロベクトルか、若しくは $v_q$ と $v$ が直交していない限り実部は 0 になりませんので、その様な特別な場合を除くと $qV$ は $V$ が存在している 3 次元部分空間上から飛び出して上位の 4 次元空間上にあるベクトルになります。
そこで 4 次元空間に行ってしまった $qV$ を何とかして元の 3 次元部分空間内に引き戻せないか考えてみましょう。
さて複素数の場合は共役複素数を更に掛けることで回転をキャンセル出来ますので、同様に $q$ の共役クォータニオン
\[ q^* = (w_q, v^*_q) \] \[ v^*_q = -v_q \]
をうまく使えば目的を果たせそうな気がします。
なお $|q|=1$なので、$q^*$ は $q$ の逆数 $q^{-1}$ でもあります。
そこで試しに $q^*$ を $qV$ の左から掛けてみましょう。
すると当たり前な気がしますが
と回転がキャンセルされて元の $V$ が復元します。
確かに元の 3 次部分空間には戻ってきましたが回転がキャンセルされては意味が無いので、次は右から $q^*$ を掛けた $qVq^*$ を考えてみましょう。
するとこの場合は感覚に反して回転はキャンセルされず、実部と虚部が次で表されるクォータニオンとなります。
ここで「$\cdot$」は内積で「$\times$」はクロス積です。
実部
\begin{align*} {\mathrm Re}[ qVq^* ] &= (-v_q \cdot v)w_q - (w_q v + v_q \times v)\cdot v^*_q \\[10pt] &= -w_q(v_q \cdot v) - w_q ( v \cdot v^*_q) - (v_q \times v)\cdot v^*_q \\[10pt] ({\text スカラー3重積を使って}) &= -w_q(v_q \cdot v) + w_q( v \cdot v_q) - (v^*_q \times v_q )\cdot v \\[10pt] &= (v_q \times v_q )\cdot v \\[10pt] &= 0 \end{align*}虚部 :
\begin{align*} {\mathrm Im}[ qVq^* ] & = (-v_q \cdot v)v^*_q + w_q(w_q v + v_q \times v) + (w_q v + v_q \times v)\times v^*_q \\[10pt] & = (v_q \cdot v)v_q + w_q^2 v + w_q(v_q \times v) + w_q (v\times v^*_q) + v_q \times v \times v^*_q \\[10pt] & = (v_q \cdot v)v_q + w_q^2 v + w_q(v_q \times v) + w_q (v_q\times v) - v_q \times v \times v_q \\[10pt] ({\text ベクトル3重積を使って}) & = (v_q \cdot v)v_q + w_q^2 v + 2 w_q(v_q \times v) - (v_q \cdot v_q )v + (v \cdot v_q) v_q \\[10pt] & = 2(v_q \cdot v)v_q + (w_q^2 - |v_q|^2)v + 2 w_q ( v_q \times v) \end{align*}この様に実部が 0 となるので $qV q^*$ は $V$ が存在している元の 3 次元部分空間上のベクトルとなります。
さらに
\[ v' = {\mathrm Im}[ qVq^* ] = 2(v_q \cdot v)v_q + (w_q^2 - |v_q|^2)v + 2 w_q ( v_q \times v) \]としたとき、
\[ |v'| = |qV q^*| = |q||V||q^*| = |V| = |v| \]
が成り立ちます。
この様に $v$ から $v'$ に座標変換しても長さが不変なので、$v'$ は 3 次元ベクトル $v$ を回転して得られた 3 次元ベクトルだということが分かります。
以上をまとめると次の事が言えます。
ある 3 次元ベクトル $v$ から実部が0のクォータニオン
\[ V = (0, v) \]
を作る。
絶対値が 1 である任意のクォータニオン $q$ に対し
を計算すると、その虚部
\[ v' = {\mathrm Im}[ qVq^* ] = 2(v_q \cdot v)v_q + (w_q^2 - |v_q|^2)v + 2 w_q ( v_q \times v) \]
は $v$ を回転させた 3 次元ベクトルになる。
ここで「$\cdot$」は内積で「$\times$」はクロス積である。
次はどの様に $v$ が回転されているかについて考えます。
その目的のために、やや恣意的ではありますがクォータニオン $q$ の実部と虚部を次の式で置き換えます。
実部 : $w_q = \cos \frac{\theta}{2}$
虚部 : $v_q = \sin \frac{\theta}{2} u$
※ ただし $u = (x_u,y_u,z_u)$ かつ $x_u^2 + y_u^2 + z_u^2 = 1$ とする(つまり単位ベクトル)
この様に置き換えても $|q| = 1$ となっていますので、任意の $q$ は上の式を使って表すことができます。
さて結論から言うと、上の様に置き換えた $q$ を使って $v'$を求めることはロドリゲスの回転公式を使って $v'$ を求めることと同等になります。
※ 証明は難しくありませんが長いので省略します
よって最終的に次の事が言えます。
ある 3 次元ベクトル $v = (x\ ,\ y\ ,\ z)$ から実部が0のクォータニオン
\[ V = (0, v) \]を作る。
さらに実数 $\theta$ と任意の単位ベクトル
\[ u = (x_u\ ,\ y_u\ ,\ z_u) \]を与えて(※ 単位ベクトルなので $x_u^2 + y_u^2 + z_u^2 = 1$)
実部 : $w_q = \cos \frac{\theta}{2}$
虚部 : $v_q = \sin \frac{\theta}{2} u$
で表されるクォータニオン $q = (w_q,v_q)$ を作る。
この時
\[ qVq^* \]を計算すると、その虚部
\[ v' = {\mathrm Im}[ qVq^* ] = 2(v_q \cdot v)v_q + (w_q^2 - |v_q|^2)v + 2 w_q ( v_q \times v) \]
は $u$ を回転軸として $\theta$ [rad] だけ $v$ を回転させて得られる 3 次元ベクトルになる。
ここで「$\cdot$」は内積で「$\times$」はクロス積である。
この公式には内積とクロス積からなる単純な演算しか含まれてないので、ロドリゲスの回転公式を使って回転させるよりクォータニオンを使って回転させた方がはるかに高速です。
そのため上の公式は至る分野で使われています。
では例を見てみましょう。
\[ v = (1 \ , \ 0 \ , \ -1) \] \[ \theta = \frac{2 \pi}{10} \] \[ u = (1/\sqrt{2} \ , \ 0 \ , \ 1/\sqrt{2}) \]
とします。
$v$ を初期位置として9回連続で回転を適用した結果が図 1 です。
確かに回転軸 $u$ を中心に $\frac{2 \pi}{10}$ [rad] の角度で回転していることが分かります。
赤い矢印 : 回転軸 $u$
大きい赤い丸 : 初期位置 $v$
小さい赤い丸 : 回転後の位置
