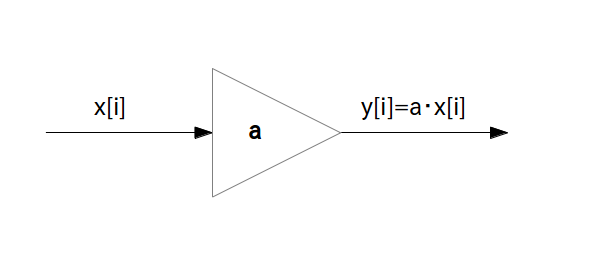
伝達関数 $\textrm{H}(z) = a$ を持つフィルタは乗算器を意味して $a$ を三角で囲んだ記号で表す
※ 四角で囲んでいる文献もあります
どの様な複雑な伝達関数を持つフィルタも実は
「乗算器」
「遅延素子」
「加算器」
と呼ばれるたった 3 つの基本パーツだけが組み合わされて出来ています。
これら基本パーツのうち「乗算器」「遅延素子」はそれ自体がディジタル線形時不変フィルタの一種なので伝達関数を持っています。
ここではこれら基本パーツの伝達関数とそれに対応するプロック図の描き方について説明します。
また基本パーツのプログラム表現についても示します。
あるフィルタのインパルス応答が $h[i] = \{a,0,0,\cdots\}$ であるとき(ここで $a$ は有限の実数)、伝達関数は $h[i]$ をZ変換して
\[ \textrm{H}(z) = a \]
となります。
この伝達関数を持つフィルタの事を「乗算器」と呼びます。
さて乗算器に $x[i]$ を入力すると、出力は畳み込み演算
\[ y[i] = \sum_{n = 0}^{\infty} \{ h[n] \cdot x[i-n] \} = a \cdot x[i] \]
が行われ、入力に $a$ が乗算された値が出てきます。
この乗算器のブロック図は次の図で表されます。
伝達関数 $\textrm{H}(z) = a$ を持つフィルタは乗算器を意味して $a$ を三角で囲んだ記号で表す
※ 四角で囲んでいる文献もあります

また乗算器はブログラムでは次のように表されます。
y[i] = a * x[i] ;
あるフィルタのインパルス応答が $h[i] = \{0,1,0,0,\cdots\}$ であるとき、伝達関数は $h[i]$ をZ変換して
\[ \textrm{H}(z) = z^{-1} \]
となります。
この伝達関数を持つフィルタの事を「(1 時刻)遅延素子」と呼びます。
さて遅延素子に $x[i]$ を入力すると出力は畳み込み演算
\[ y[i] = \sum_{n = 0}^{\infty} \{ h[n] \cdot x[i-n] \} = x[i-1] \]が行われ、1 時刻前の入力の値が遅れて出てきます。
この遅延素子のブロック図は次の図で表されます。
伝達関数 $\textrm{H}(z) = z^{-1}$ は遅延素子を意味して $z^{-1}$ を四角で囲んだ記号で表す

また遅延素子はブログラムでは次のように表されます。
y[i] = x[i-1] ;
$x_0[i]$ から $x_{(\textrm{M}-1)}[i]$ まで計 $\textrm{M}$ 個の入力信号 $x_n$ があるとき、それらを足しあわせて
\begin{align*} y[i] = \sum_{n=0}^{\textrm{M}-1} x_n[i] \end{align*}を出力するパーツを「加算器」と呼びます。
加算器は厳密に言うと次のページで説明する「並列結合」であってフィルタではありません。
従って加算器に伝達関数はありませんがブロック図は次の様に表されます。
加算器は+記号を丸で囲む。
※ 四角で囲んでいる文献もあります
※ +ではなくて SUM や Σ 記号を使う文献もあります
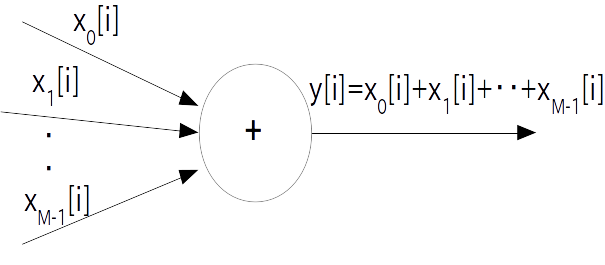
また加算器はブログラムでは次のように表されます。
x[ n ][ i ] を n 番目の入力信号の時刻 i における値とすると
y[i] = 0 ; for( int n = 0; n < M; ++n ) y[i] += x[ n ][ i ] ;