2. 多層パーセプトロン(MLP)とは

動物の脳は多数(人間の大脳の場合140億個位)の「神経細胞」という細胞がシナプス結合されて出来ています。
そこでまず研究者達はこの「神経細胞」を数学的にモデル化した「パーセプトロン」を考案しました。

※ 文献によってはパーセプトロンの事を「ユニット」や「ノード」と呼ぶこともあります

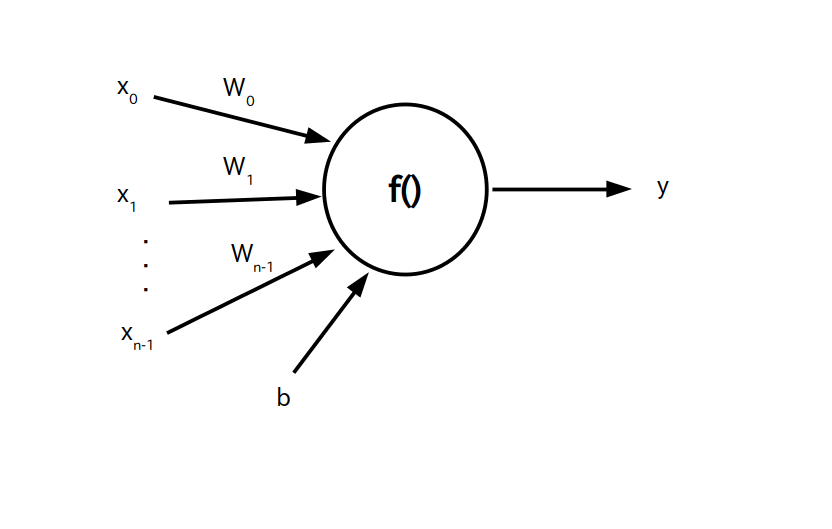
さてパーセプトロンは

$n$ 個の入力信号に対し 1 個の信号を出力する関数

$f()$ であり、以下の数式で表すことができます。
この

$f()$ の事を「活性化関数」と呼びます。

定義: パーセプトロンの式:

$\begin{align*} y &= f \left ( \sum_{i=0}^{n-1} \{w_i\cdot x_i\} + b \right ) \\ &= f \left ( w_0\cdot x_0 + \cdots + w_{n-1}\cdot x_{n-1} + b \right ) \end{align*}$

$y$ : 出力信号

$f()$ : 活性化関数

$x_i$ : $i$ 番目の入力信号、 $(i=0,1,\cdots,n-1)$

$w_i$ : 変数、 $i$ 番目の入力信号に掛けられる重み(weight)と呼ぶ

$b$ : 変数、バイアス(bias)と呼ぶ

またパーセプトロンは以下の様なグラフで表すことが出来ます。

図1. パーセプトロンのグラフ

※ データフロー・グラフではなくて一般的なグラフ表現です

2. 多層パーセプトロン(MLP)

次に研究者達は「パーセプトロン」を多数結合して「多層パーセプトロン(MLP: Multi-Layer Perceptron)」と呼ばれるネットワークを考えました。

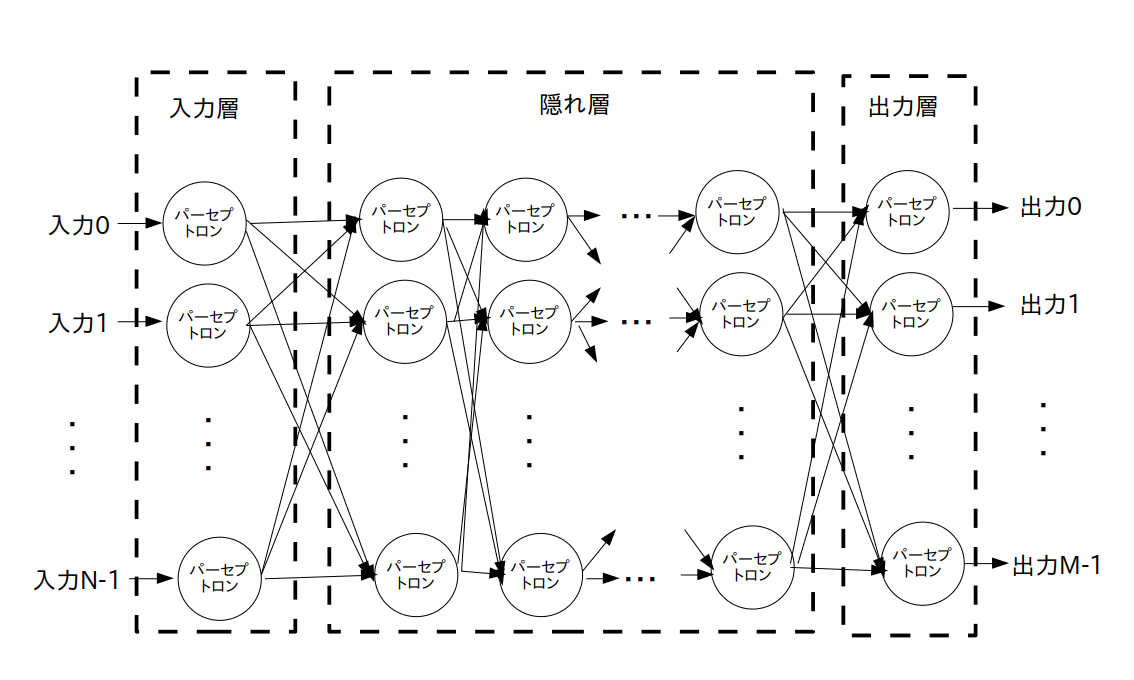
MLP は「入力層(Input Layer)」、「隠れ層(Hidden Layer, 中間層とも言う)」、「出力層(Output Layer)」ごとに層(Layer)分けされた多層構造になっています。
各層は更に多数の層に分かれている場合もあります。

そして MLP の各層間のパーセプトロンは全て互いに結合しているような構造になっています。
この様な構造を持つニューラルネットワークの事を「全結合型(Fully Connected)ニューラルネットワーク」と呼びます。

まとめると、MLP の構造は図 2 で示される「全結合型フィードフォワードニューラルネットワーク」となっています。

図2. 多層パーセプトロン(MLP) の構造 = 全結合型フィードフォワードニューラルネットワーク

※ データフロー・グラフではなくて一般的なグラフ表現です

3. 3層ニューラルネットワーク

さらに話を簡単にするため、今回は MLP として隠れ層が 1 層だけで出来ている「3 層ニューラルネットワーク」を扱いたいと思います(図3)。

※ 正確には「3 層全結合型フィードフォワードニューラルネットワーク」ですが、長いので単に「3層ニューラルネットワーク」とだけ書きます

図3. 3層ニューラルネットワークの構造

※ データフロー・グラフではなくて一般的なグラフ表現です

入力層(Input Layer)が N 個、隠れ層(Hidden Layer)が K 個、出力層(Output Layer)が M 個のパーセプトロンで出来ている

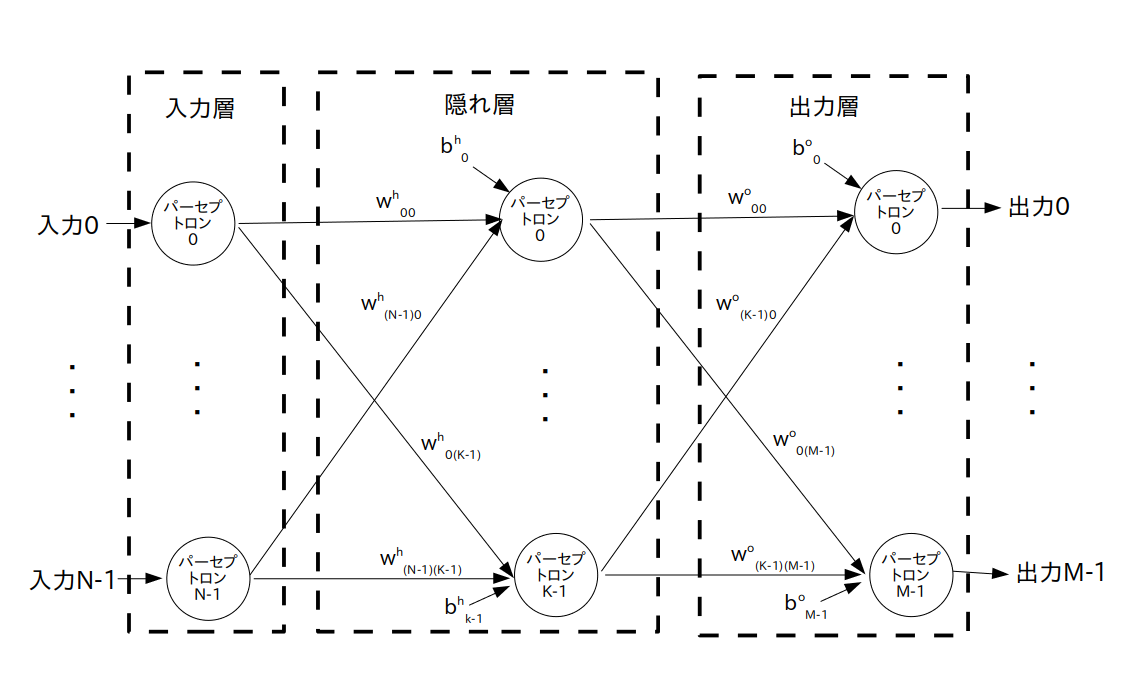
$w_{ij}^{\textrm h}$ ・・・入力層のパーセプトロン No. $i$ の出力信号から、隠れ層のパーセプトロン No. $j$ への入力に掛けられる重み

$b_{j}^{\textrm h}$ ・・・隠れ層のパーセプトロン No. $j$ のバイアス

および

$w_{ij}^{\textrm o}$ ・・・隠れ層のパーセプトロン No. $i$ の出力信号から、出力層のパーセプトロン No. $j$ への入力に掛けられる重み

$b_{j}^{\textrm o}$ ・・・出力層のパーセプトロン No. $j$ のバイアス

GetTitle()2. 多層パーセプトロン(MLP)とは

1. パーセプトロン