3. フーリエ変換の例

Processing math: 8%

3. フーリエ変換の例

(例1) デルタ関数(インパルス信号) $\delta(t)$

超関数であるデルタ関数(インパルス信号) $\delta(t)$ のフーリエ変換は

$\begin{align*} \textrm{F}(w) &= \int_{-\infty}^{\infty} \left \{ \delta(t) \cdot \textrm{e}^{\{- j \cdot w \cdot t \}} \right \} \textrm{d}t \\[10pt] (\text{デルタ関数の性質より}) &= \textrm{e}^{0} \\[10pt] &= 1 \end{align*}$

です。

(例2) 複素正弦波 $\textrm{e}^{\{j \cdot w_1 \cdot t \}}$

複素正弦波

$f(t) = \textrm{e}^{\{j \cdot w_1 \cdot t \}}$

は $|f(t)| = 1$ なので絶対可積分ではありませんが、超関数であるデルタ関数を使えばフーリエ変換を求められます。
具体的には

$\begin{align*} \textrm{F}(w) &= \int_{-\infty}^{\infty} \left \{ \textrm{e}^{\{ j \cdot w_1 \cdot t \}} \cdot \textrm{e}^{\{- j \cdot w \cdot t \}} \right \} \textrm{d}t \\[10pt] &= \int_{-\infty}^{\infty} \left \{ \textrm{e}^{ j \cdot ( w_1 -w ) \cdot t } \right \} \textrm{d}t \\[10pt] &= \lim_{a \rightarrow \infty} \left [ \frac{ \textrm{e}^{ j ( w_1 - w ) \cdot t } }{ j \cdot ( w_1 - w ) } \right ]^a_{-a} \\[10pt] &= \lim_{a \rightarrow \infty} \left \{ \frac{ \textrm{e}^{ j \cdot ( w_1 -w ) \cdot a } }{ j ( w_1 -w) } - \frac{ \textrm{e}^{ -j \cdot ( w_1 -w ) \cdot a } }{ j ( w_1 -w) } \right \} \\[10pt] &= 2\pi\cdot \lim_{a \rightarrow \infty} \left \{ \frac{ 1 }{ \pi \cdot ( w - w_1) } \cdot \frac{ \textrm{e}^{ j \cdot ( w -w_1 ) \cdot a } - \textrm{e}^{ j \cdot ( w - w_1 ) \cdot a } }{ 2\cdot j } \right \} \\[10pt] &= 2\pi\cdot \lim_{a \rightarrow \infty} \left \{ \frac{ \sin \{ ( w-w_1) \cdot a \} }{ \pi \cdot ( w - w_1) } \right \} \\[10pt] (\text{デルタ関数の定義より}) &= 2\pi\cdot \delta( w - w_1 ) \\[10pt] \end{align*}$

となります。

(例3) $f(t)=1$

$f(t)=1$

は絶対可積分ではありませんが、超関数であるデルタ関数を使えばフーリエ変換を求められます。
具体的には例2で $w_1=0$ とした場合なので

$\textrm{F}(w) = 2\pi\cdot\delta(w)$

となります。
ちなみにこれは $2\pi\cdot\delta(w)$ を逆フーリエ変換することでも証明できます。
具体的には次の通りです。

$\begin{align*} f(t) &= \frac{1}{2\pi} \int_{-\infty}^{\infty} \left \{ 2\pi\cdot\ \delta(w) \cdot \textrm{e}^{\{ j \cdot w \cdot t \}} \right \} \textrm{d}w \\[10pt] (\text{デルタ関数の性質より}) &= \textrm{e}^{0} \\[10pt] &= 1 \end{align*}$

(例4) 三角関数 $\cos (w_1 \cdot t)$ と $\sin(w_1 \cdot t)$

cos と sin は絶対可積分ではありませんが、超関数であるデルタ関数を使うとフーリエ変換を求められます。
まず cos の方ですが

$f(t) = \cos (w_1 \cdot t) = \frac{ \textrm{e}^{ \{ j \cdot w_1 \cdot t \} } + \textrm{e}^{\{ -j \cdot w_1 \cdot t \} } }{2}$

なので、例2より

$\textrm{F}(w) = \pi \cdot \{ \delta(w-w_1) + \delta(w+w_1) \}$

がすぐ求まります。

同様に sin については

$f(t) = \sin (w_1 \cdot t) = \frac{ \textrm{e}^{ \{ j \cdot w_1 \cdot t \} } - \textrm{e}^{\{ -j \cdot w_1 \cdot t \} } }{2\cdot j}$

なので、例2より

$\textrm{F}(w) = \frac{\pi}{j} \cdot \{ \delta(w-w_1) - \delta(w+w_1) \}$

です。

(例5) 単一パルス

$a > 0$ を有限な値とした時、単一パルス

$f(t) = \begin{cases} 0 \ & t <0 \\[10pt] 1 \ & 0 \leq t \leq a \\[10pt] 0 & t > a \end{cases}$

はもちろん絶対可積分なので普通にフーリエ変換が求められます。

$\begin{align*} \textrm{F}(w) &= \int_{0}^{a} \left \{ \textrm{e}^{\{- j \cdot w \cdot t \}} \right \} \textrm{d}t \\[10pt] &= \left [ \frac{\textrm{e}^{\{- j \cdot w \cdot t \}}}{-j\cdot w} \right ]^a_0 \\[10pt] &= \frac{1 - \textrm{e}^{\{- j \cdot w \cdot a \} }}{j\cdot w} \end{align*}$

ちなみに $w=0$ の時はロピタルの定理を使って

$\textrm{F}(0) = \frac{j\cdot a \cdot \textrm{e}^0 }{j} = a$

です。

(例6) 指数減衰 $\textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)$

$\sigma > 0$ とし、 $u(t)$ を単位ステップ関数

$u(t)= \begin{cases} 0 \ & t < 0 \\[10pt] 1 & t \geq 0 \end{cases}$

とした時、指数減衰

$f(t) = \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)$

はもちろん絶対可積分なので普通にフーリエ変換が求められます。

$\begin{align*} \textrm{F}(w) &= \int_{-\infty}^{\infty} \left \{ \textrm{e}^{\{ - \sigma \cdot t \}} \cdot u(t) \cdot \textrm{e}^{\{- j \cdot w \cdot t \}} \right \} \textrm{d}t \\[10pt] &= \int_{0}^{\infty} \left \{ \textrm{e}^{ -( \sigma + j \cdot w ) \cdot t } \right \} \textrm{d}t \\[10pt] &= \lim_{a \rightarrow \infty} \left [ \frac{ \textrm{e}^{ -( \sigma + j \cdot w ) \cdot t } }{ -( \sigma + j \cdot w ) } \right ]^a_{0} \\[10pt] &= \lim_{a \rightarrow \infty} \left [ \frac{ \textrm{e}^{ - \sigma \cdot a } \cdot \textrm{e}^{ - j \cdot w \cdot a } }{ -( \sigma + j \cdot w ) } \right ] + \frac{ 1 }{ \sigma + j \cdot w } \\[10pt] \end{align*}$

ここで $\sigma > 0$ より、上の第1項は0に収束するので

$\textrm{F}(w) = \frac{ 1 }{ \sigma + j \cdot w }$

となります。

(例7) 単位ステップ関数

単位ステップ関数

$u(t)= \begin{cases} 0 \ & t < 0 \\[10pt] 1 & t \geq 0 \end{cases}$

のフーリエ変換は例 6 で $\sigma \rightarrow 0$ とすることで

$\textrm{F}(w) = \frac{ 1 }{ j \cdot w }$

となります。
ただし $w=0$ の時は発散するので $w \ne 0$ の範囲だけで考える必要があります。

(別解)

フーリエ変換の性質より

$\frac{\textrm{d}}{\textrm{d}t}\ u(t)$

のフーリエ変換は

$j\cdot w \cdot \textrm{F}(w)$

で、

$\frac{\textrm{d}}{\textrm{d}t}\ u(t) = \delta(t)$

なので、両辺をフーリエ変換すると例1より

$j\cdot w \cdot \textrm{F}(w) = 1$

よって

$\textrm{F}(w) = \frac{ 1 }{ j \cdot w }$

となります。

(例8) 正弦波の指数減衰 $\sin(w_1 \cdot t) \cdot \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)$

ある信号 $f(t)$ のフーリエ変換を $\textrm{F}(w)$ 、別の信号 $g(t)$ のフーリエ変換を $\textrm{G}(w)$ とします。
すると畳み込みの定理より $h(t) = f(t)\cdot g(t)$ のフーリエ変換は

$\begin{align*} \textrm{H}(w) &= \frac{1}{2\pi} \cdot \left ( \textrm{F} * \textrm{G} \right ) (w) \\[10pt] &= \frac{1}{2\pi} \cdot \int^{\infty}_{-\infty} \textrm{F}(\xi) \cdot \textrm{G} (w-\xi) \ \textrm{d}\xi \end{align*}$

となります。
ここで特に

$\textrm{G} (w) = \delta( w + a)$

の時は

$\begin{align*} \textrm{H}(w) &= \frac{1}{2\pi} \cdot \int^{\infty}_{-\infty} \textrm{F}(\xi) \cdot \delta (w+a-\xi) \ \textrm{d}\xi \\[10pt] &= \frac{1}{2\pi} \cdot \int^{\infty}_{-\infty} \textrm{F}(\xi) \cdot \delta (\xi - (w+a)) \ \textrm{d}\xi \\[10pt] &= \frac{\textrm{F}(w+a)}{2\pi} \end{align*}$

よって例4と例6から正弦波の指数減衰

$f(t) = \sin(w_1 \cdot t) \cdot \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)$

は(ただし $\sigma > 0$ )

$\begin{align*} \textrm{F}(w) &= \frac{\pi}{2\pi \cdot j}\cdot \left \{ \frac{1}{\sigma + j\cdot (w-w_1)} - \frac{1}{\sigma + j\cdot (w+w_1)} \right \} \\[10pt] &= \frac{1}{2j}\cdot \frac{ (\sigma + j\cdot w + j\cdot w_1) - (\sigma + j\cdot w - j\cdot w_1) } { (\sigma + j\cdot w - j\cdot w_1)\cdot (\sigma + j\cdot w + j\cdot w_1 ) } \\[10pt] &= \frac{1}{2j}\cdot \frac{ 2\cdot j\cdot w_1 }{ (\sigma + j\cdot w)^2 + w_1^2 } \\[10pt] &= \frac{ w_1 }{ (\sigma + j\cdot w)^2 + w_1^2 } \\[10pt] \end{align*}$

となります。

(例9) 時刻 0 から始まって $n$ 回振動したら 0 になる正弦波

正弦波 $\sin(w_1\cdot t)$ の周期を $\textrm{T} = 2\pi/w_1$ [秒] とします。
$n$ を 1 以上の整数としたとき次の信号を考えます。

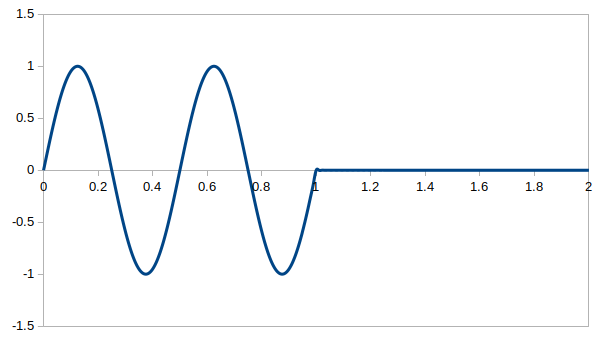
$f(t) = \begin{cases} 0 & t < 0 \\[10pt] \sin(w_1\cdot t) \ & 0 \leq t \leq n\cdot \textrm{T} \\[10pt] 0 & t > n\cdot \textrm{T} \end{cases}$

例えば、 $w_1 = 4\pi$ [rad/秒]、 $\textrm{T} = 1/2$ [秒]、 $n = 2$ [回]の場合は次のグラフになります。

図1: $f(t)$ のグラフ例

$w_1 = 4\pi$ [rad/秒]、 $\textrm{T} = 1/2$ [秒]、 $n = 2$ [回]

今回考える $f(t)$ は例5で考えた単一パルス(ただし $a = n\cdot \textrm{T}$ )を sin にかけた式になっていますので、例8と同様にデルタ関数の畳込み演算を利用できます。
具体的には例4と例5より

$\begin{align*} \textrm{F}(w) &= \frac{\pi}{2\pi\cdot j}\cdot \left \{ \frac{1-\textrm{e}^{\{- j \cdot (w-w_1) \cdot n\cdot \textrm{T} \} }}{j\cdot (w-w_1)} - \frac{1-\textrm{e}^{\{- j \cdot (w+w_1) \cdot n\cdot \textrm{T} \} }}{j\cdot (w+w_1)} \right \} \\[10pt] &= \frac{1}{2\cdot j}\cdot \left \{ \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot \textrm{e}^{ \{ j \cdot w_1 \cdot n\cdot \textrm{T} \} } }{j\cdot (w-w_1)} - \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot \textrm{e}^{ \{ -j \cdot w_1 \cdot n\cdot \textrm{T} \} } }{j\cdot (w+w_1)} \right \} \\[10pt] (\text{$w_1 = 2\pi/\textrm{T}$より})&= \frac{1}{2\cdot j}\cdot \left \{ \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot \textrm{e}^{ \{ j \cdot 2 \pi \cdot n \} } }{j\cdot (w-w_1)} - \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot \textrm{e}^{ \{ -j \cdot 2 \pi \cdot n \} } }{j\cdot (w+w_1)} \right \} \\[10pt] (\text{$n$は整数だから})&= \frac{1}{2\cdot j}\cdot \left \{ \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot 1 }{j\cdot (w-w_1)} - \frac{ 1- \textrm{e}^{ \{ -j \cdot w \cdot n\cdot \textrm{T} \} } \cdot 1 }{j\cdot (w+w_1)} \right \} \\[10pt] &= \frac{1}{2\cdot j}\cdot \left \{ \frac{ 1 }{j\cdot (w-w_1)} - \frac{ 1 }{j\cdot (w+w_1)} \right \} \cdot \left ( 1- \textrm{e}^{ \{ -j \cdot n\cdot \textrm{T} \cdot w \} } \right ) \\[10pt] &= \frac{1}{-2}\cdot \left \{ \frac{ (w+w_1) - (w-w_1) }{(w-w_1)\cdot (w+w_1)} \right \} \cdot \left ( 1- \textrm{e}^{ \{ -j \cdot n\cdot \textrm{T} \cdot w \} } \right ) \\[10pt] &= \left \{ \frac{w_1}{-w^2+w_1^2} \right \} \cdot \left ( 1- \textrm{e}^{ \{ -j \cdot n\cdot \textrm{T} \cdot w \} } \right ) \\[10pt] \end{align*}$

となります。
なお $w = \pm w_1$ の時はロピタルの定理より

$\begin{align*} \textrm{F}(\pm w_1) &= \lim_{w \rightarrow \pm w_1} \frac{w_1}{-2w} \cdot \left ( j \cdot n \cdot \textrm{T} \cdot \textrm{e}^{ \{ - j \cdot n \cdot \textrm{T} \cdot w \} } \right ) \\[10pt] &= \mp \frac{1}{2} \cdot \left ( j \cdot n \cdot \textrm{T} \cdot \textrm{e}^{ \{ \mp j \cdot n \cdot 2 \pi \} } \right ) \\[10pt] &= \mp \frac{j \cdot n \cdot \textrm{T}}{2} \end{align*}$

です。

GetTitle()3. フーリエ変換の例

(例1) デルタ関数(インパルス信号) δ(t)\delta(t)

(例2) 複素正弦波 e{j⋅w1⋅t}\textrm{e}^{\{j \cdot w_1 \cdot t \}}

(例3) f(t)=1f(t)=1

(例4) 三角関数 \cos (w_1 \cdot t)\cos (w_1 \cdot t) と \sin(w_1 \cdot t)\sin(w_1 \cdot t)

(例5) 単一パルス

(例6) 指数減衰 \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)\textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)

(例7) 単位ステップ関数

(例8) 正弦波の指数減衰 \sin(w_1 \cdot t) \cdot \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)\sin(w_1 \cdot t) \cdot \textrm{e}^{ \{ -\sigma \cdot t \} } \cdot u(t)

(例9) 時刻 0 から始まって nn 回振動したら 0 になる正弦波