前ページの例で使用した $z(t)$ の絶対値 $|z(t)| = t$ は時間を表す変数 $t$ [秒]によって変化していますが、偏角 $\angle \ z(t) = \pi/4$ [rad] は $t$ [秒] によって変化していませんでした。
今度は逆に絶対値 $|z(t)|$ は $t$ [秒] によって変化しないけれど偏角 $\angle \ z(t)$ は変化する複素信号を考えます。

その様な複素信号の例はいくらでもありますが、その一つとしてここでは「(時間領域)複素正弦波」又は「複素指数関数」について学びます。


定義： 定義: (時間領域)複素正弦波、または複素指数関数 \[ z(t) = \left \{ a \cdot \textrm{e}^{\{j \cdot \phi\}} \right \} \cdot \textrm{e}^{\{j \cdot w \cdot t \}} \]

を(時間領域)複素正弦波、または複素指数関数と呼び、複素平面の上の回転運動体となる。


$a$・・・振幅(または半径)、実数の定数、範囲は実数全体(ただし一般的には $a \geq 0$ )、単位は扱う信号の種類による(ボルトとかアンペアとか度とかetc.)

$\phi$ (ファイ) ・・・初期位相、実数の定数、範囲は $-\pi \leq \phi \leq \pi$、単位は [rad]

$w$ ・・・角周波数(または角速度)、実数の定数、範囲は実数全体、単位は [rad/秒]

$t$ ・・・時刻、実数の変数、単位は[秒]

この複素正弦波は初期位置

\[ z(0) = \left \{ a \cdot \textrm{e}^{\{j \cdot \phi\}} \right \} \]

が与えられた時、時刻 $t$ において $w\cdot t$ [rad] だけ $z(0)$ を回転させて得られる複素信号です。
言い換えれば $z(t)$ は $z(0)$ からスタートして角周波数 $w$ [rad/秒]の速さで半時計回りに回転する回転運動体になります。
なお $w$ が負の場合は時計回りに逆回転します。

またアナログサイン波と同様に「角周波数」「周波数」「周期」は以下の変換式を使って相互変換可能です。
ただし複素正弦波の場合は上で書いた通り逆回転時に角周波数 $w$ が負になることもあるので、周期を求める際に角周波数と周波数の絶対値を取る必要があります。

公式：角周波数、周波数、周期の相互変換式

(注) 周期 T は正の実数なので $f$ と $w$ の絶対値を取る必要があります

\[ w = 2\pi \cdot f \] \[ f = \frac{w}{2\pi} \] \[ \textrm{T} = \frac{1}{|f|} = \frac{2\pi}{|w|} \]

では例として

振幅 : $a = 2$

初期位相が $\phi = \pi/4$ [rad]

角周波数 : $w = \pi/2$ [rad/秒]

である複素正弦波

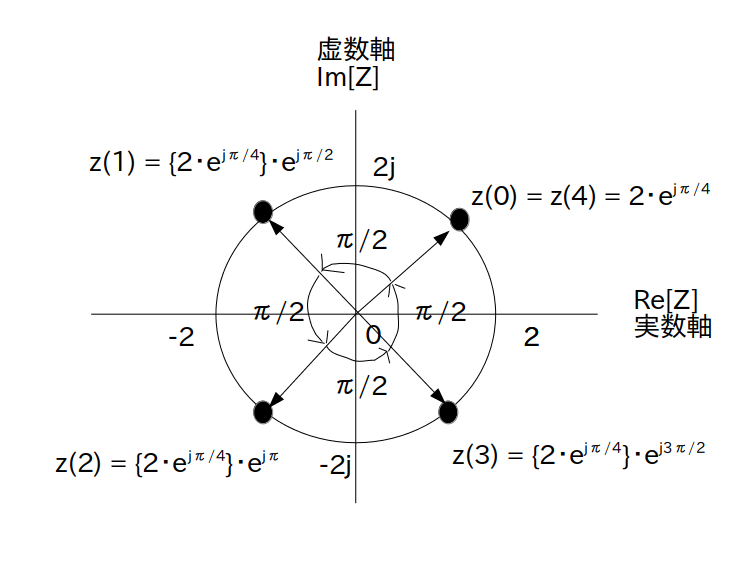
\[ z(t) = \left \{ 2 \cdot \textrm{e}^{\{j \cdot \pi/4 \}} \right \} \cdot \textrm{e}^{\{j \cdot \pi/2 \cdot t \}} \]

を図1に示します。
参考までに $z(0)$、$z(1)$、$z(2)$、$z(3)$、$z(4)$の位置も示しています。
この例の複素正弦波は初期位置

\[ z(0) = 2 \cdot \textrm{e}^{\{j \cdot \pi/4 \}} \]

からスタートし、 $w = \pi/2$ [rad/秒] の角速度で回転している運動体となっていることが分かります。

図1: 複素正弦波の例 \[ z(t) = \left \{ 2 \cdot \textrm{e}^{\{j \cdot \pi/4 \}} \right \} \cdot \textrm{e}^{\{j \cdot \pi/2 \cdot t \}} \]

(補足) 角周波数と角速度

上では $w$ を角周波数と書きましたが、正確には角速度(angular velocity)と言います。
一方、角周波数の正式な定義は角速度の絶対値

角周波数 = |角速度|

です。
よって本来ならば負の角周波数というものは存在しませんが、時間領域のサイン波と用語を統一したかったので、今回のアクティビティではあえて角速度と角周波数という用語を混同して使っています。

角速度についてもう少し詳しく説明しましょう。
角速度は回転運動体の座標ベクトル $r$ と速度ベクトル $v$ から

\[ w = \frac{r \times v}{|r|^2} \]

で定義されます。
ここで式中の $\times$ はクロス積です。

この様に角速度はクロス積で求めますので、角速度は2次元平面上ではスカラー、3次元空間以上の空間上ではベクトルとなります。

※ クロス積の結果はベクトルなので厳密には2次元平面では定義されないのですが、2次元平面の場合は $r$ を $v$ に重ねる時の回転方向が半時計回りなら正、時計回りなら負であるスカラーがクロス積の結果になります。

さて複素平面は実質的に 2次元平面(正確には2 次元ユークリッド空間 $\textrm{R}^2$)と同一視できますので複素正弦波の角速度も上の定義から求めることが出来るはずです。
まず回転運動体の角速度を $w$ [rad/秒]、座標ベクトルを $r$ とすると、微小時間 $\textrm{d}t$ [秒] で運動体が進む距離は円弧の長さの公式より $|r| \cdot w\cdot \textrm{d}t$ になります。
なお角速度の符号は正(反時計回り)とします。

一方、回転運動体の(ある瞬間における)速度ベクトルを $v$ とすると、微小時間 $\textrm{d}t$ [秒] で運動体が進む距離は $|v| \cdot \textrm{d}t$ で近似することが出来ます。
ここで $r$ と $v$ は直交していますので

\[ |v| = \frac{|r|\cdot|v|}{|r|} = \frac{|r|\cdot|v|\cdot \sin(\pi/2)}{|r|} = \frac{|r \times v|}{|r|} \]

となりますが、角速度の符号は正(反時計回り)としたので

\[ |v| = \frac{r \times v}{|r|} \]

となります。
以上より

\[ w = \frac{|v| \cdot \textrm{d}t}{|r|\cdot \textrm{d}t} = \frac{r \times v}{|r|^2} \]

が求まります。
なお時計回り回転の場合は角速度の符号が負になるだけです。