フィルタの直列結合、並列結合、フィードバック機構について学びましたので、いよいよ基本パーツを使って複雑な伝達関数を持つフィルタのブロック図を描く用意が出来ました。
ここでは伝達関数からブロック図への変換例をいくつか紹介したいと思います。
またそのプログラム表現についても紹介します。


(例1) 乗算器と乗算器の直列結合

\begin{align*} \textrm{H}(z) = a \cdot b \end{align*}

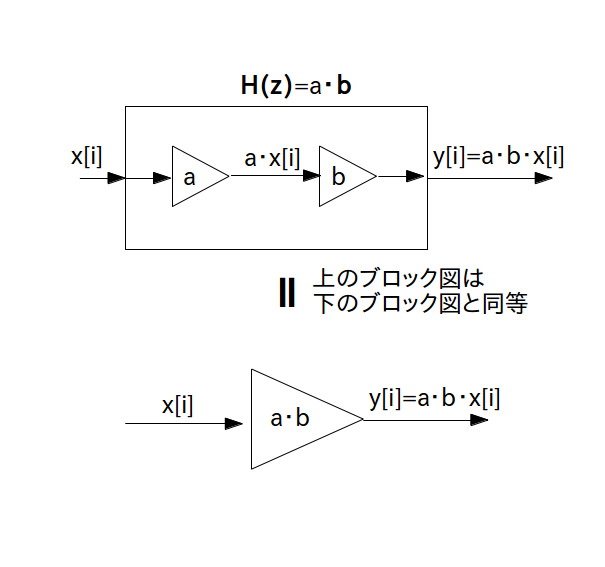
という伝達関数を持つフィルタは乗算器 $\textrm{H}_1(z) = a$ と乗算器 $\textrm{H}_2(z) = b$ の直列結合と考えられますので結局乗算器 1 つだけのブロック図に変わります。

この時のブロック図は次の通りです。

例1のブロック図

　

プログラム表現は次の通りです。

例1のプログラム表現 (C言語): 
y[i] = (a * b) *  x[i] ;

(例2) 乗算器と 1 時刻遅延素子の直列結合

\begin{align*} \textrm{H}(z) = a \cdot z^{-1} \end{align*}

という伝達関数を持つフィルタは乗算器 $\textrm{H}_1(z) = a$ と 1 時刻遅延素子 $\textrm{H}_2(z) = z^{-1}$ の直列結合と考えられます

この時のブロック図は次の通りです。
なお乗算器は遅延素子の後に置くことが多いのでこの図では乗算器と遅延素子の順番を入れ替えています(もちろん乗算器 → 遅延素子の順でも問題ないです)。

例2のブロック図

　

プログラム表現は次の通りです。

例2のプログラム表現 (C言語): 
y[i] = a * x[i-1] ;

(例3) 2 つの 1 時刻遅延素子の直列結合 (2 時刻遅延素子)

\begin{align*} \textrm{H}(z) = z^{-1} \cdot z^{-1} \end{align*}

という伝達関数を持つフィルタは 1 時刻遅延素子 $\textrm{H}_1(z) = z^{-1}$ と 1 時刻遅延素子 $\textrm{H}_2(z) = z^{-1}$ の直列結合になりますが、これを $z$ の項でまとめると伝達関数は

\begin{align*} \textrm{H}(z) = z^{-2} \end{align*}

となります。

この伝達関数を持つフィルタを「2 時刻遅延素子」と呼び、入力が 2 時刻遅れて出てくるフィルタになります。
2時刻遅延素子の時のブロック図は次の通りです。

例 3 のブロック図

　

プログラム表現は次の通りです。

例3 のプログラム表現 (C言語): 
y[i] = x[i-2] ;

(例4) $n$ 個の 1 時刻遅延素子の直列結合 ($n$ 時刻遅延素子)

同様に遅延素子を $n$ 個の 1 時刻遅延素子を直列結合することで「$n$ 時刻遅延素子」が作られます。
伝達関数は次の通りです。

\begin{align*} \textrm{H}(z) = z^{-n} \end{align*}

ブロック図は次の通りです。

例 4 のブロック図

　

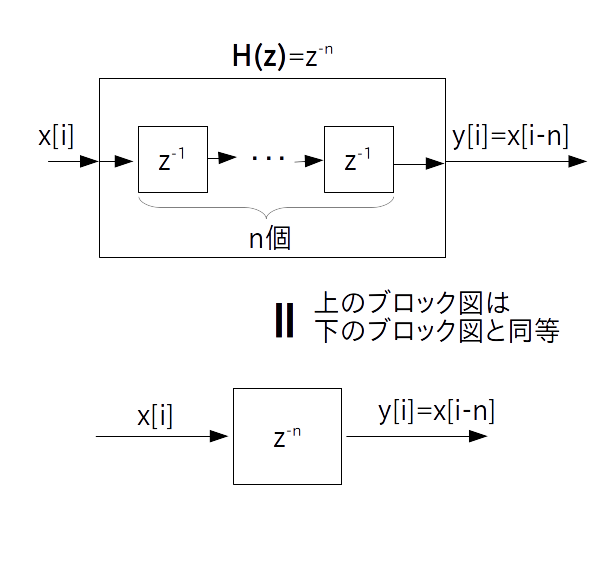
プログラム表現は次の通りです。

例4 のプログラム表現 (C言語): 
y[i] = x[i-n] ;

(例5) 直列結合と並列結合の組み合わせ (ディレイフィルタ)

\begin{align*} \textrm{H}(z) = a + b \cdot z^{-n} \end{align*}

という伝達関数を持つフィルタは乗算器 $\textrm{H}_1(z) = a$ と 乗算器 $b$ と $n$ 時刻遅延素子 $z^{-n}$ を直列結合した $\textrm{H}_2(z) = b \cdot z^{-n}$ の並列結合となっています。
このフィルタのことを「ディレイフィルタ(delay filter)」といいます。

この時のブロック図は次の通りです。

例5のブロック図

　

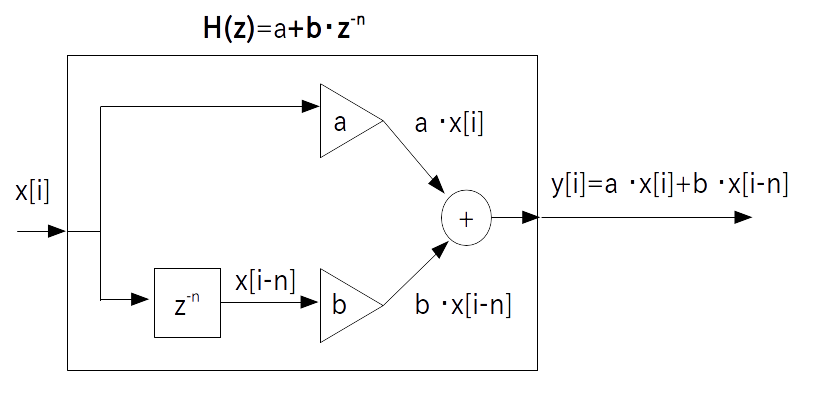
プログラム表現は次の通りです。

例5のプログラム表現 (C言語): 
y[i] = a * x[i] + b * x[i-n] ;

(例6) 遅延素子+乗算器の並列結合

\begin{align*} \textrm{H}(z) = a \cdot z^{-2} + b \cdot z^{-3} \end{align*}

という伝達関数を持つフィルタは 2 時刻遅延素子+乗算器の $\textrm{H}_1(z) = a\cdot z^{-2}$ と 3 時刻遅延素子+乗算器の $\textrm{H}_2(z) = b \cdot z^{-3}$ の並列結合と考えられます

このフィルタのブロック図を素直に描くと次の通りになります。

例6のブロック図(素直な描き方)

　

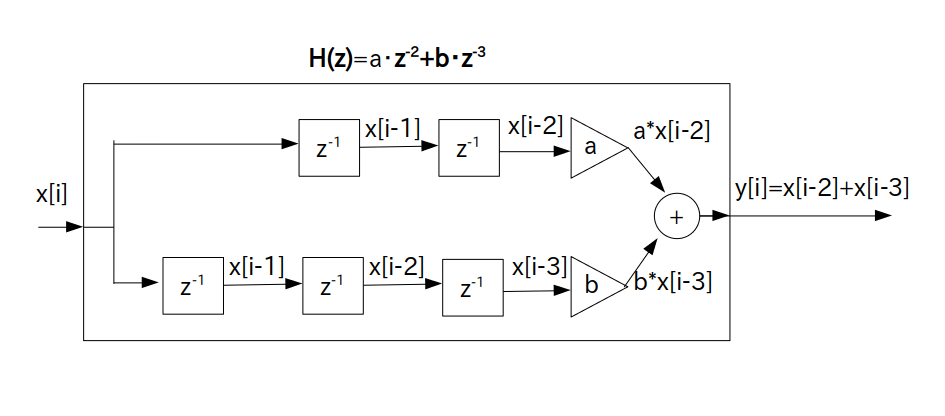
ただし、このままだと遅延素子が無駄に多く含まれていてもったいないので、遅延素子を一部共通化して次の様なブロック図に出来ます。

例6のブロック図(遅延素子を共通化した描き方)

　

プログラム表現は次の通りです。

例6のプログラム表現 (C言語): 
y[i] = a*x[i-2] + b*x[i-3] ;

(例7) 遅延素子+乗算器とフィードバック機構の組み合わせ

\begin{align*} \textrm{H}(z) = \frac{1}{1- a \cdot z^{-1}} \end{align*}

という伝達関数を持つフィルタは 1 時刻遅延素子+乗算器で出来たフィルタをフィードバック機構の $\textrm{H}_1(z)$ としたフィルタであると考えられます。

従ってブロック図は次の通りになります。

例7のブロック図

　

プログラム表現は次の通りです。

例7のプログラム表現 (C言語): 
y[i] =  x[i] + a * y[i-1] ;