次に IIR ハイパスフィルタの設計を行います。
まずベースとなるアナログハイパスフィルタは以下の回路図で表されるCRハイパスフィルタになります。
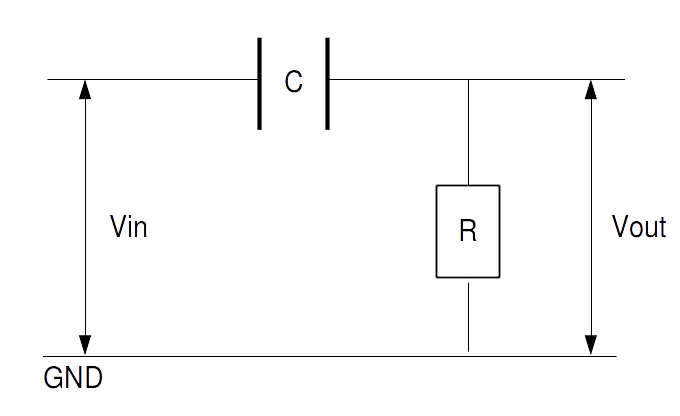
まず CR ハイパスフィルタの(アナログ)伝達関数と周波数特性とインパルス応答はそれぞれ以下の通りになります。
カットオフ角周波数を $w_c = \frac{1}{RC}$ [rad/秒] とする。
\begin{align*} \textrm{H}(s) & = \frac{ 1 }{ 1 + \frac{w_c}{s} } \\ & = \frac{ s }{ s + w_c } \\ \end{align*}※ 導出方法については前ページを参考
よって振幅特性(ゲイン)と位相特性はそれぞれ
\[ |\textrm{H}(w)| = \frac{ w }{ \sqrt{w^2 + w_c^2 }} \] \[ \angle \textrm{H}(w) = \tan^{-1}(w/w_c) \]$s/(s-a)$の逆ラプラス変換は $\delta(t) + \frac{ \textrm{d} }{\textrm{dt}} \textrm{e}^{at} = \delta(t) + a \cdot \textrm{e}^{at} $ なので、伝達関数を逆ラプラス変換すると
※ $\delta(t)$ はディラックのデルタ関数
\begin{align*} h(t) & = \delta(t) - w_c \cdot \textrm{e}^{-w_c\cdot t} \end{align*}よって IIR ハイパスフィルタのインパルス応答は次の様になります。
$\tau$ [秒] をサンプリング間隔とした時、
\begin{align*} h[i] = \tau \cdot h(\tau \cdot i ) = \tau \cdot \delta( \tau \cdot i ) - \tau \cdot w_c \cdot \textrm{e}^{-w_c \cdot \tau \cdot i} \end{align*}ただし $\tau \cdot \delta( \tau \cdot i )$ をプログラミングで扱うのは困難なのでディジタルインパルス信号 $\delta[i]$ で置き換えて
\begin{align*} h[i] = \delta[i] - \tau \cdot w_c \cdot \textrm{e}^{-w_c \cdot \tau \cdot i} \end{align*}よって IIR ハイパスフィルタの伝達関数は次の様になります。
(求め方)
インパルス応答の両辺を Z 変換して
\begin{align*} \textrm{H}(z) &= \sum_{i=0}^\infty \{ \delta[i] \cdot z^{-i} \} - \sum_{i=0}^\infty \{ \tau \cdot w_c \cdot \textrm{e}^{-w_c \cdot \tau \cdot i} \cdot z^{-i} \} \\ &= 1 - \sum_{i=0}^\infty \{ \tau \cdot w_c \cdot \textrm{e}^{-w_c \cdot \tau \cdot i} \cdot z^{-i} \} \\ &= 1 - \tau \cdot w_c \cdot \sum_{i=0}^\infty \{ \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} \}^i \\ \end{align*}右辺の第2項はIIR ローパスパスフィルタの伝達関数にマイナスを掛けた値なので
\begin{align*} \textrm{H}(z) &= 1 - \frac{ \tau \cdot w_c }{ 1 - \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} } \\ &= \frac{ 1 - \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} - \tau \cdot w_c }{ 1 - \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} } \\ &= \frac{ (1 - \tau \cdot w_c ) - \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} }{ 1 - \textrm{e}^{-w_c \cdot \tau} \cdot z^{-1} } \\ \end{align*}これより、フィルタ係数は以下の通りになります。
なお IIR ハイパスフィルタの周波数特性もIIR ローパスパスフィルタと同様に、カットオフ角周波数とサンプリング間隔が充分に小さければ 1次 CR ハイパスフィルタの周波数特性に近似されますが、カットオフ角周波数が高くなるにつれてエイリアシングの影響でかなり特性が歪んでくるので慎重に設計する必要があります。