data : 入力信号、 1 x N 行列 (定数テンソル)

では 3 層ニューラルネットワークを データフロー・グラフ化して TensorFlow で構築してみましょう。
まず入力信号を考えます。
入力信号全体の名前を data とすると、今考えている 3 層ニューラルネットワークの入力層のパーセプトロンの個数は N 個でしたので、 data は実数の 1xN 行列(=テンソル)
\[ {\rm data} = \begin{bmatrix} d_{0}\ , & \cdots &, d_{N-1} \\ \end{bmatrix} \]
で表すことができます。
data の i 列目の値 $d_i$ が入力層のパーセプトロン No.i に入力される信号になります。
よって TensorFlow では入力信号は図 1 の様に 1 x N 行列の定数テンソルで定義されます。
data : 入力信号、 1 x N 行列 (定数テンソル)

次に入力層を考えます。
前ページの図3から入力層だけを切り出したのが以下の図2です。
※ データフロー・グラフではなくて一般的なグラフ表現です
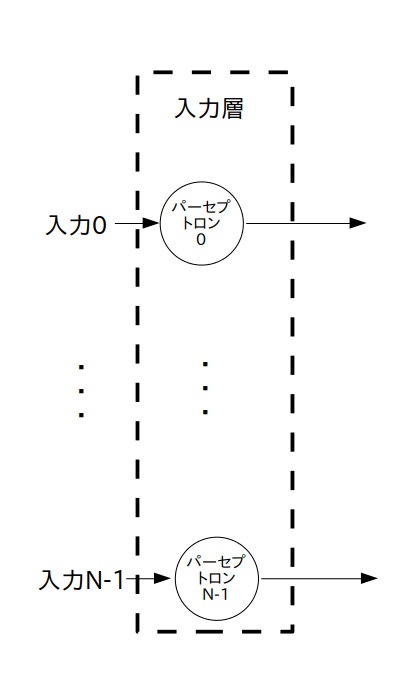
この様に、入力層は入力されたデータをそのままスルーして出力するだけなので、データフロー・グラフは図3の様になります。
入力信号 data をスルーして隠れ層にそのまま渡すだけ(つまり何もしない)
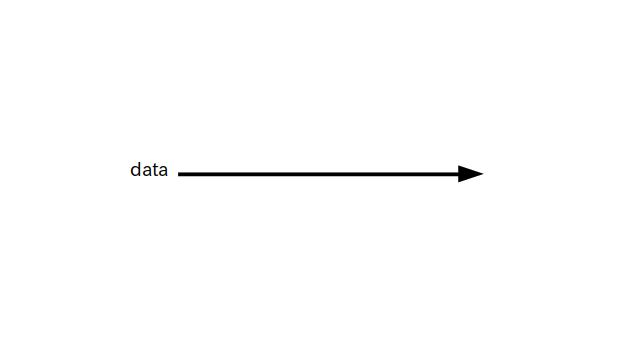
次に隠れ層を考えます。
前ページの図3から入力層と隠れ層を切り出したのが以下の図4です。
※ データフロー・グラフではなくて一般的なグラフ表現です

$w_{ij}^{\rm h}$ ・・・ 入力層のパーセプトロン No.$i$ の出力信号から、隠れ層のパーセプトロン No.$j$ への入力に掛けられる重み
$b_{j}^{\rm h}$ ・・・ 隠れ層のパーセプトロン No.$j$ のバイアス
隠れ層は K 個のパーセプトロンで出来ていて、それぞれのパーセプトロンは入力層からの出力信号を受取ります。
その際に重みが入力に掛けられ、更にバイアスが足されます。そして最後に活性化関数 $f()$ に通して出力されます。
さて入力層はニューラルネットワークへの入力信号をそのままスルーしてただけですので、入力層のパーセプトロン No.$i$ から出力される信号は $d_i$ となります。
よって隠れ層のパーセプトロン No.$j$ の出力 $y_j^{\rm h}$ は以下の式で表されます。
\[ y_j^{\rm h} = f \left ( \sum_{i=0}^{\rm N-1} \{w_{ij}^{\rm h}\cdot d_i\} + b_j^{\rm h} \right ) \ , \ (j=0,1,\cdots,{\rm K-1}) \]
次にこの式を行列の形に書き直します。
まず隠れ層の出力信号全体を表す行列を y_h とすると、y_h は 1xK 行列
\[ {\rm y\_h} = [y_0^{\rm h}\ , \cdots,\ y_{\rm K-1}^{\rm h}] \]
で表されます。
隠れ層の重み全体を表す行列を w_h とすると、w_h は NxK 行列
\[ {\rm w\_h} = \begin{bmatrix} w_{00}^{\rm h}\ , & \cdots &,\ w_{\rm 0(K-1)}^{\rm h} \\ \vdots & \ddots & \vdots \\ w_{\rm (N-1)0}^{\rm h}\ , & \cdots &,\ w_{\rm (N-1)(K-1)}^{\rm h} \end{bmatrix} \]
で表されます。
隠れ層のバイアス全体を表す行列を b_h とすると、b_h は 1xK 行列
で表されます。
また活性化関数 $f()$ には色々な種類がありますが、今回は双曲線正接(tanh)関数を使いたいと思います。
すると隠れ層の出力信号は以下の行列演算で求められます。
y_h = tanh( data・w_h + b_h )
「・」は行列積
tanh(x) は行列の全ての要素に対して演算
ではこの行列演算を元に隠れ層をデータフロー・グラフ化してみましょう。
まず重み w_h とバイアス b_h はディープラーニングにより値が変化しますので、定数テンソルではなく変数テンソル として定義します(図5)。
w_h : 隠れ層の重み、 N x K 行列 (変数テンソル)
b_h : 隠れ層のバイアス、1 x K 行列 (変数テンソル)
※ w_h と b_h の各要素は乱数で初期化する
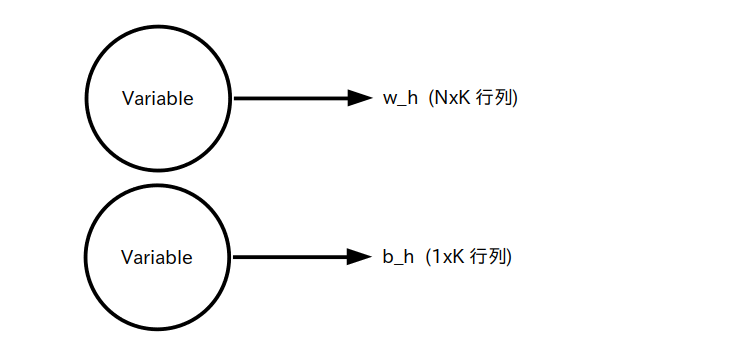
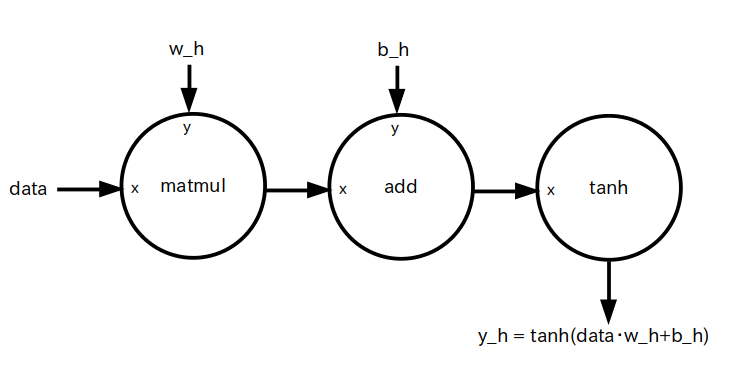
すると隠れ層は上で挙げた行列演算の式より図 6 のようなデータフロー・グラフになります。
入力層からの出力信号( = 入力信号) data と w_h の行列積 data・w_h を求め、それに b_h を足し、双曲線正接(tanh)に通して y_h に出力する
最後に出力層を考えます。
前ページの図3から隠れ層と出力層を切り出したのが以下の図4です。
※ データフロー・グラフではなくて一般的なグラフ表現です

$w_{ij}^{\textrm o}$ ・・・ 隠れ層のパーセプトロン No.$i$ の出力信号から、出力層のパーセプトロン No.$j$ への入力に掛けられる重み
$b_{j}^{\textrm o}$ ・・・ 出力層のパーセプトロン No.$j$ のバイアス
出力層は M 個のパーセプトロンで出来ていて、それぞれのパーセプトロンは隠れ層からの出力信号を受取ります。
その際に重みが入力に掛けられ、更にバイアスが足されます。
そして最後に活性化関数 $f()$ に通して出力されます。
つまりパーセプトロンの数と活性化関数が異なるだけで出力層も隠れ層と同じ様な構造となります。
そこで出力層の重み全体を表す行列を w_o とすると、w_o は KxM 行列
\[ {\rm w\_o} = \begin{bmatrix} w_{00}^{\rm o}\ , & \cdots &,\ w_{\rm 0(M-1)}^{\rm o} \\ \vdots & \ddots & \vdots \\ w_{\rm (K-1)0}^{\rm h}\ , & \cdots &,\ w_{\rm (K-1)(M-1)}^{\rm o} \end{bmatrix} \]
で表されます。
出力層のバイアス全体を表す行列を b_o とすると、b_o は 1xM 行列
で表されます。
また次のページで詳しく説明しますが、今回は「多クラス分類問題」を扱う予定なので活性化関数 $f()$ として softmax 関数を使います。
すると出力層の出力信号は以下の行列演算で求められます。
y_o = softmax( y_h・w_o + b_o )
「・」は行列積
ではこの行列演算を元に出力層をデータフロー・グラフ化してみましょう。
まず隠れ層の時と同様に、重み w_o とバイアス b_o はディープラーニングにより値が変化しますので、定数テンソルではなく変数テンソル として定義します(図8)。
w_o : 出力層の重み、 K x M 行列 (変数テンソル)
b_o : 出力層のバイアス、1 x M 行列 (変数テンソル)
※ w_o と b_o の各要素は乱数で初期化する

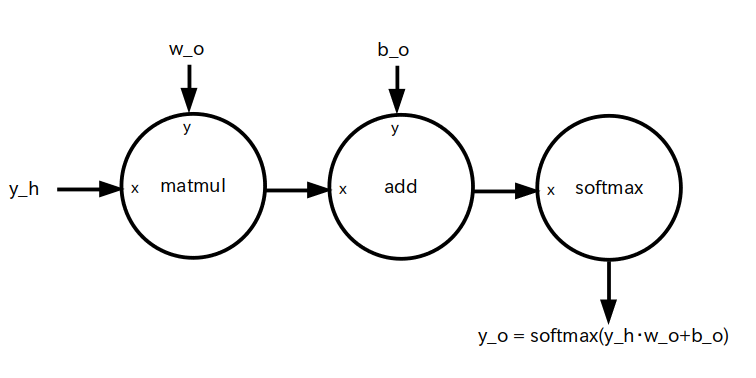
すると出力層のデータフロー・グラフは図 9 となります。
隠れ層からの出力信号 y_h と w_o の行列積 y_h・w_oを求め、それに b_o を足し、softmax 関数に通し、y_o に代入する
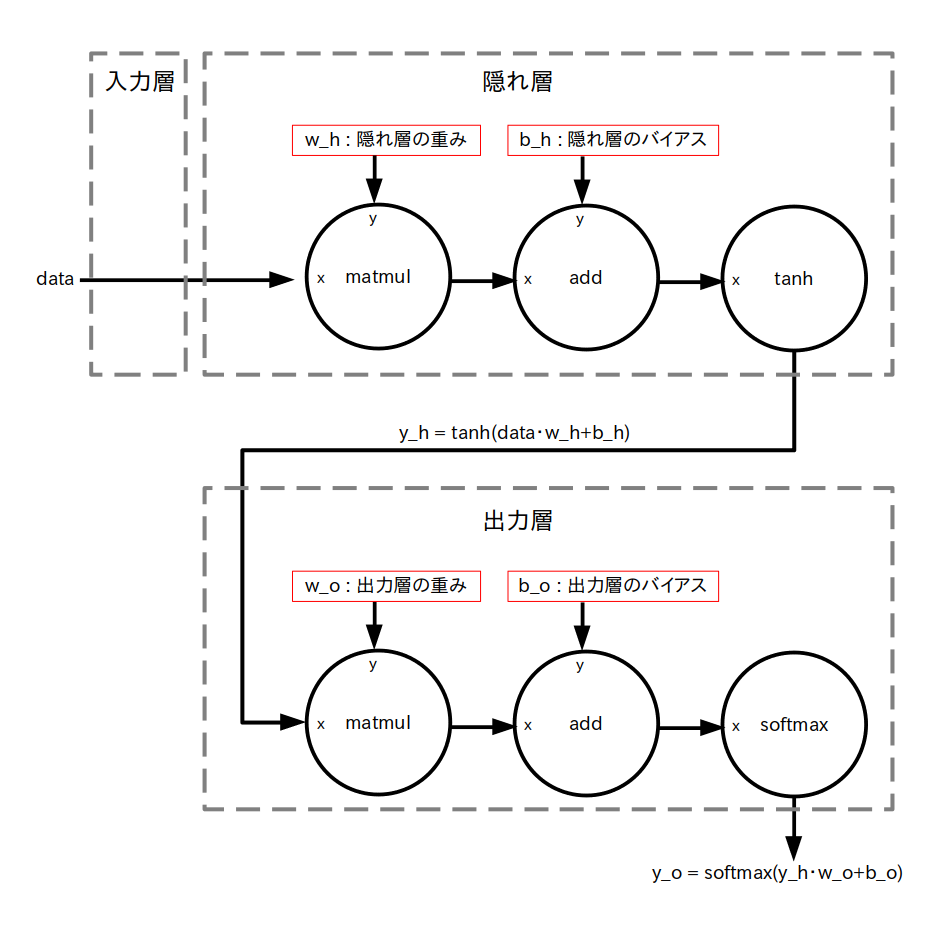
以上の各層のデータフロー・グラフを組み合わせると、3層ニューラルネットワーク全体では次のようなデータフロー・グラフとなります。
後はこのデータフローを元に TensorFlow で 3層ニューラルネットワークを構築するだけです。