4. TensorFlowによるMLPの学習

前ページで 3 層ニューラルネットワークを構築しました。
ただし隠れ層と出力層の重みやバイアス( w_h、b_h、w_o、b_o の4つの変数) を乱数で初期化していましたので、入力信号 data を入力しても全く意味の無い出力信号 y_o が出力されます。

したがって、何らかの入力信号を与えた時に理想的な出力がされるように「ディープラーニング」を使ってニューラルネットワークを学習させる必要があります。

ところで与えられた画像をニューラルネットワークを使って「猫」とか「犬」とか「鳥」みたいな種類(クラス)別に画像を分類する問題を考えます。
この様な問題を「多クラス分類問題」と呼びます。

それで、この多クラス分類問題を扱う場合は理想的な出力信号のことを「ラベル」と呼んでいます。
今回のアクティビティでは「多クラス分類問題」を取り扱いますので、これ以降は理想的な出力信号のことをラベルと呼びます。

また適切に学習を行うためには学習用入力信号とラベルの組を複数用意する必要があります。
学習用入力信号とラベルの組の全体集合を「学習データセット」と呼びます。

※ 文献によっては「訓練データセット」とか「教師データセット」と呼ぶこともあります

今回は学習データセットのサイズを L 、つまりデータセット内に入力信号とラベルの組が No.0 から No.(L-1) まで L 組あることにします。

2. 学習用入力信号

学習用入力信号全体の名前を data_training とすると、学習データセットのサイズが L で、今考えている 3 層ニューラルネットワークの入力層のパーセプトロンの個数は N 個でしたので、 data_training は LxN 行列

「data_training の j 行 i 列目の値 $t_{\rm ji}$ は学習データセットの No.j 番目に属し、入力層のパーセプトロンの No.i 番目に入力される入力信号の値」

学習データセットの No.0 番目の入力信号は [1,2]
学習データセットの No.1 番目の入力信号は [3,4]
学習データセットの No.2 番目の入力信号は [5,6]

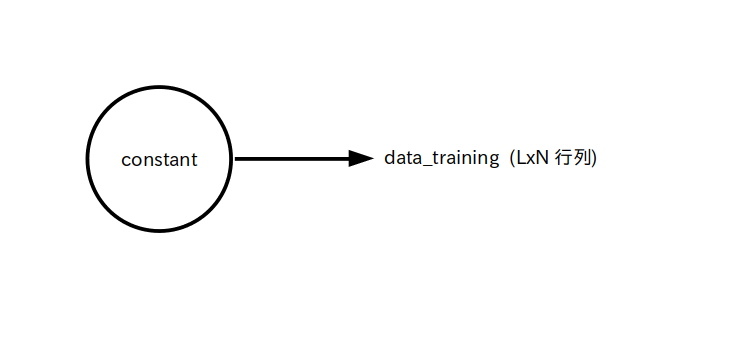
という訳で、 TensorFlow では学習用入力信号は図 1 の様に L x N 行列の定数テンソルで定義されます。

図1: 学習用入力信号

data_training : 学習用入力信号、 L x N 行列 (定数テンソル)

※ $t_{\rm ji}$ : 学習データセット No.j に属し、入力層のパーセプトロン No.i に入力される入力信号の値

3. 学習用ラベル

今考えている 3 層ニューラルネットワークの出力層のパーセプトロンの個数は M 個で、学習データセットのサイズは L としましたので、学習用ラベル全体の名前を label_training とすると、label_training は LxM 行列

「label_training の j 行 i 列目の値 $l_{\rm ji}$ は学習データセットの No.j に属し、出力層のパーセプトロンの No.i から出力される理想的な値(ラベル)」

さて、このラベルの値をどのように決めるかについては色々な形式が考えられますが、今回は「one-hot ベクトル形式」を使いたいと思います。

one-hot ベクトル形式とは、入力した信号があるクラスに属する場合は 1、それ以外は 0 とする様にラベルを決める形式です。
ラベルの形式としてこの one-hot ベクトルを使うと、

「label_training の j 行 i 列目の値 $l_{\rm ji}$ は学習データセットの No.j 番目の学習用入力信号がクラス No.i に属してる(=1)、属していない(=0)」

では例としてニューラルネットワークに入力した画像や音声信号を「猫」と「犬」と「鳥」の 3 クラスに分類したい場合を考えてみます。
今回は猫をクラス No.0、犬をクラス No.1、鳥をクラス No.2 とすることにすると、各ラベルは

猫ラベル(クラス No.0)・・・ [1,0,0]
犬ラベル(クラス No.1)・・・ [0,1,0]
鳥ラベル(クラス No.2)・・・ [0,0,1]

で表されます。
なおクラス数が 3 つなので出力層のパーセプトロンの数は M = 3 に自動的に決まります。

学習データセットの No.0 番目の入力信号は猫[1,0,0]である
学習データセットの No.1 番目の入力信号は犬[0,1,0]である
学習データセットの No.2 番目の入力信号は猫[1,0,0]である
学習データセットの No.3 番目の入力信号は鳥[0,0,1]である
学習データセットの No.4 番目の入力信号は犬[0,1,0]である

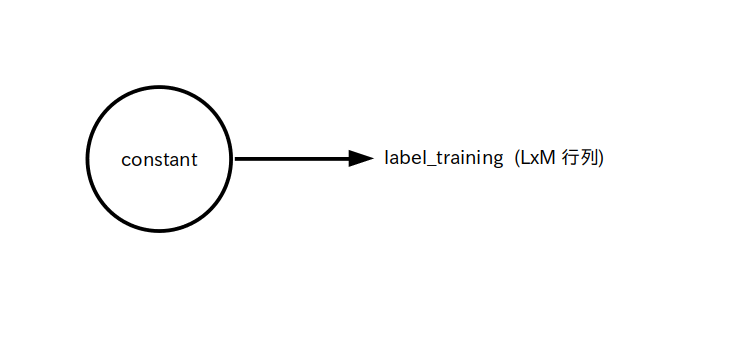
という訳でラベル label_training は図 2 の様に L x M 行列の定数テンソルで定義されます。

図2: ラベル

label_training : 学習用ラベル、 L x M 行列 (定数テンソル)

※ $l_{\rm ji}$ : 学習データセット No.j に属する学習用入力信号がクラス No.i に属してるか(=1)、属していないか(=0)

4. 予測値

さて学習用入力信号 data_training は行列でしたので、data_training を 3 層ニューラルネットワークに入力して出てくる出力信号も行列になります。
この行列のことを「予測値」とか「予測結果」と呼びます。

ここで予測値の名前を predict とすると、predict は label_training と同様に LxM 行列

ところで今回は出力層のパーセプトロンの活性化関数をsoftmax 関数としたため

「predict の j 行 i 列目の値 $p_{\rm ji}$ は学習データセットの No.j 番目に属する学習用入力信号がクラス No.i に属する確率」

No.0 番目の入力信号: 猫の確率 80 %、犬の確率 10 %、鳥の確率 10 %
No.1 番目の入力信号: 猫の確率 25 %、犬の確率 70 %、鳥の確率 5 %
No.2 番目の入力信号: 猫の確率 50 %、犬の確率 35 %、鳥の確率 15 %
No.3 番目の入力信号: 猫の確率 10 %、犬の確率 40 %、鳥の確率 50 %
No.4 番目の入力信号: 猫の確率 1 %、犬の確率 97 %、鳥の確率 2 %

5. 損失関数

学習データセットを用意したら、次は重みとバイアス( w_h、b_h、w_o、b_o の4つの変数)をディープラーニングにより学習します。

ただし何らかの指標が無いと正しく学習されているか分かりませんので、まずその指標を決める必要があります。
この指標の事を「損失関数(loss function)」、損失関数の戻り値を「損失(loss)」と呼びます。

この損失関数には色々な種類がありますが、今回は多クラス分類問題でよく使われている「カテゴリカル・クロスエントロピー(categorical cross entropy)」を利用したいと思います。

カテゴリカル・クロスエントロピーは上で定義した学習用ラベル(label_training)と予測値(predict)の要素 $l_{ji}$ と $p_{ji}$ を使って次の様に定義されます。

定義: カテゴリカル・クロスエントロピーの定義

\[ {\rm entropy} = -\sum_{j=0}^{\rm L-1} \sum_{i=0}^{M-1} l_{ji}\log p_{ji} \]

という性質を持っていますので、entropy が可能な限り小さくなる様に重みとバイアスの値を学習・更新すれば良い事が分かります。

さて上の定義式は総和演算を使って次のような行列演算で表すことができます。

カテゴリカル・クロスエントロピーの行列演算

予測確率 predict を log を通し、ラベル label_training と掛け合わせる、さらに総和演算をして -1 倍して entropy に出力する

entropy = - reduce_sum( log(predict)*label_training )

※ * は行列積ではなくてただの掛け算

※ 最後に -1 倍するのを良く忘れるので注意

従ってカテゴリカル・クロスエントロピーの演算を predict の計算部分も含めてデータフロー・グラフ化すると次のようになります。

図3: カテゴリカル・クロスエントロピーのデータフロー・グラフ

6. 最適化アルゴリズム

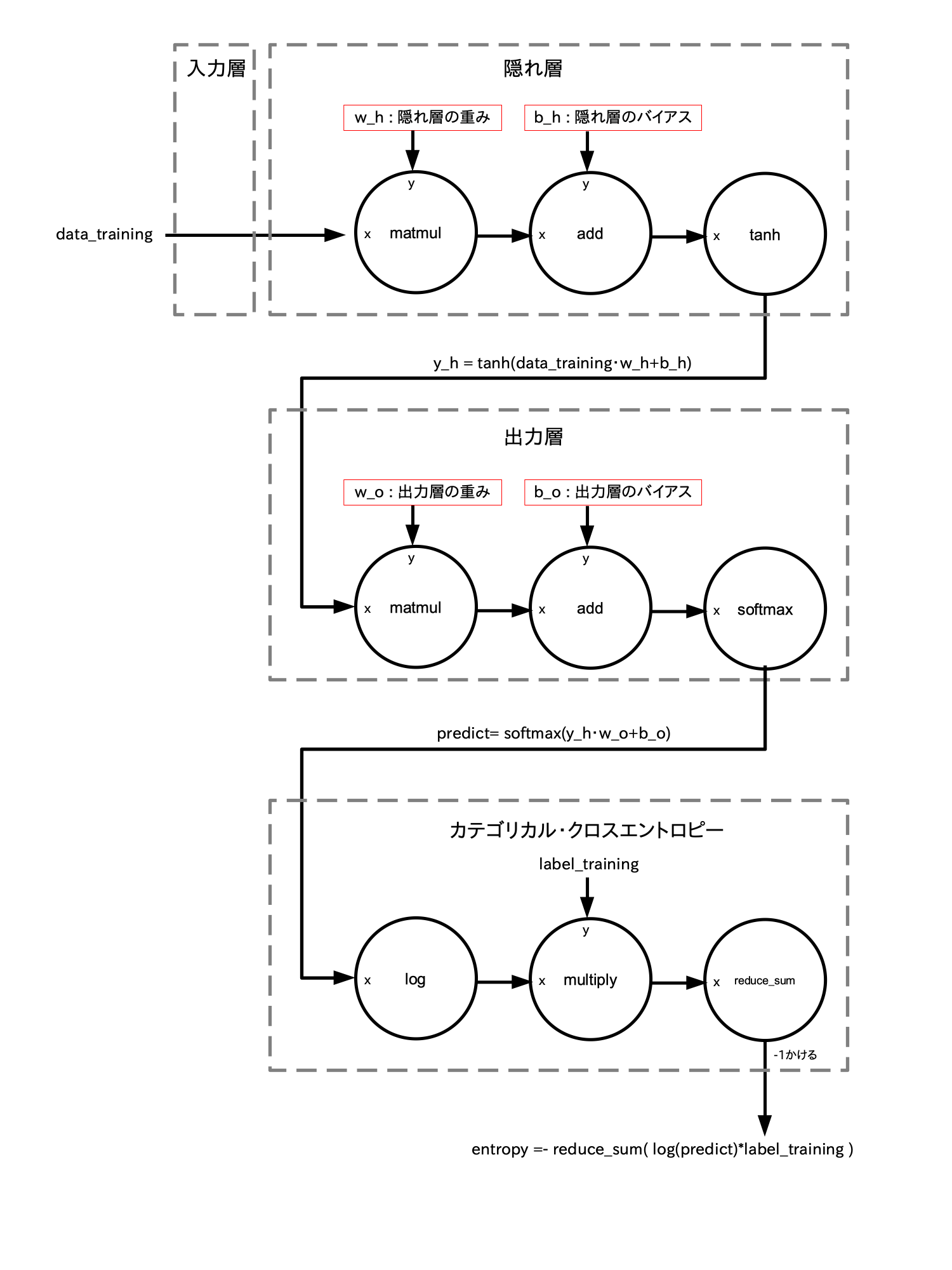
さて損失が小さくなるように重みやバイアスを学習して更新するアルゴリズムを最適化アルゴリズムと呼びます。

最適化アルゴリズムには色々な種類があるのですが、今回は

の 2 つを取り扱います。
※ SGD は学習の収束速度が遅いので Adam が使われることが多いようです

この SGD や Adam を実行するためは非常に難しい数学の知識が必要なのですが、幸いなことに TensorFlow ではクラスとして既に用意されているので誰でも簡単に利用できます。

SGD クラスと Adam クラス

SGD クラス: tf.keras.optimizers.SGD

Adam クラス: tf.keras.optimizers.Adam

ソース内に出てくる「 learning rate = 0.1 」の数値 0.1 を「学習率」と呼び、学習の精度と速度を表しています。
学習率の値が大きいほどニューラルネットワークは適当に学習しますが速く学習が進みます。
逆に値が小さいとニューラルネットワークはきちんと学習しますが遅く学習が進みます。
いずれにしろ 1 回では学習は終わりませんので、損失関数の値が十分小さくなるまで何回も学習を繰り返す必要があります。

さてこの例では学習対象である変数 x と y の初期値をそれぞれ 1,0 と-0.5、損失関数を ${\rm loss}() = x^2+y^2$、学習率を 0.1、学習回数を 50 回としたとき、損失を最小にする x と y の値(正解は x=0, y=0)を Adam を使って求めています。

ソース 1: Adam による学習例

import tensorflow as tf

# 学習対象の変数
x = tf.Variable([[1]], dtype=tf.float32)
y = tf.Variable([[-0.5]], dtype=tf.float32)

#損失関数
@tf.function
def loss():
    return x**2 + y**2  # ** は乗

print(f'損失={loss()}');
print(f'x={x.numpy()}');
print(f'y={y.numpy()}');
print('')

opt = tf.keras.optimizers.Adam( learning_rate=0.1 ) # Adam使用、学習率 0.1
#opt = tf.keras.optimizers.SGD( learning_rate=0.1 ) # SGD を使いたい場合はこちら
for i in range(50):  # 学習を50回繰り返す
    opt.minimize(lambda: loss(), [x,y])  #学習を1回実施。lambda は損失関数の名前、[x,y]は学習対象の変数
    
print('学習結果')
print(f'損失={loss()}');
print(f'x={x.numpy()}');
print(f'y={y.numpy()}');
print('')

結果は以下のようになります。
学習を50回繰り返すと損失が十分小さくなり、 (x,y) の値が損失関数の戻り値を最小にする (0,0) に近づいていることが分かります。

ソース 1 の結果

損失=[[1.25]]
x=[[1.]]
y=[[-0.5]]

学習結果
損失=[[0.0007694]]
x=[[-0.00481909]]
y=[[-0.02731627]]

7. ミニバッチ学習

実際のディープラーニングでは学習データセットのサイズ L は膨大な数となるため、学習データセット全てを使って一気に学習を行うことは滅多にありません。

ではどうするかというと、学習データセットを更に「バッチ(batch)」と呼ばれるサブ学習データセットに細かく分割し、バッチ単位で学習を行います。
この学習方法のことを「ミニバッチ学習」といいます。

またバッチに含まれる入力信号とラベルの組の個数を「バッチサイズ」と呼び、慣習的には 32,64,128,256,・・・・など 2 の n 乗の数が良く使われています。

なお、学習データセットのサイズとバッチサイズが同じ場合を「バッチ学習」、バッチサイズが 1 の場合を「オンライン学習」と言います。

ところで学習データセットのサイズが L でしたのでバッチは総数 L/B 個あります( L が B で割り切れない場合は今回は考えないことにします)。
バッチ No.0 から順にバッチ No.(L/B)-1 まで全てのバッチを使って一通り学習を済ませることを「エポック(epoch)」と呼び、エポックの繰り返し回数のことを「エポック数」と呼びます。
例えばエポック数が 3 で、学習データセットのサイズが L =6、バッチサイズが B=2 の時はバッチが3つあるので次の様にして学習が繰り返されます。

学習開始
↓
(エポック 0 開始) バッチNo.0を使って学習 → バッチNo.1 を使って学習 → バッチNo.2 を使って学習 (エポック 0 終了)
↓
(エポック 1 開始) バッチNo.0を使って学習 → バッチNo.1 を使って学習 → バッチNo.2 を使って学習 (エポック 1 終了)
↓
(エポック 2 開始) バッチNo.0を使って学習 → バッチNo.1 を使って学習 → バッチNo.2 を使って学習 (エポック 2 終了)
↓
エポックを 3 回繰り返したので学習終了

さてバッチの分割の仕方も色々考えられるのですが、今回は単純に学習データセットの先頭から順に取り出すことにします。
つまりバッチサイズを B としたとき、バッチ No.k の入力信号は BxN 行列

8. ディープラーニングの実行

では全ての準備が整ったのでいよいよディープラーニングを実行してみましょう。

今回考えている 3 層ニューラルネットワークの場合、学習対象の変数は w_h、b_h、w_o、b_o の4つですので、結局のところ次のように書けばディープラーニングが実行されます。

ソース 2: ディープラーニングの実行

opt = tf.keras.optimizers.Adam( learning_rate=r )
for e in range(E):
    for k in range(int(L/B)):
        print(f'\repoch {e} batch {k}', end='')
        data_training_k = data_training[B*k:B*k+B]
        label_training_k = label_training[B*k:B*k+B]
        opt.minimize(lambda: loss(data_training_k,label_training_k), [w_h,b_h,w_o,b_o])

※1 r : 学習率
※2 E : エポック数
※3 L : 学習データセットのサイズ
※4 B : バッチサイズ
※5 data_training, label_training : 学習用入力信号とラベル
※6 w_h, b_h, w_o, b_o : 隠れ層の重み、隠れ層のバイアス、出力層の重み、出力層のバイアス
※7 loss(data_training_k,label_training_k) : 図3のカテゴリカル・クロスエントロピー

9. 検証データセットとテストデータセット

いままでは学習データセットだけを考えていましたが、実際にディープラーニングを実行する場合は「検証データセット」と「テストデータセット」というデータセットも必要です。

検証データセットは学習データセットの様に検証用入力信号とそれに対応するラベルが組になっているデータセットです。
同様にテストデータセットもテスト用入力信号とそれに対応するラベルが組になっているデータセットです。

学習データセットだけ使って評価してしまうと「過学習(オーバーフィッティング)」が生じてしまい、実際のデータに適合していないモデルが出来てしまうことがあります。

そこで検証データセットも学習中に併用し、過学習が起きてないか常に確認しながら慎重に学習を進める必要があります。
そしてもし過学習が生じてしまっている場合は、パラメータの数を見直したり、場合によってはモデルそのものを見直して最初から学習をやり直す必要があります。

さらに、学習データセットと検証データセットを使って無事に学習を終えたとしても、テストデータセットの損失が大きい場合は最終チェックに不合格ということですので、これまたパラメータの数やモデルを見直して最初から学習と検証をやり直す必要があります。

10. 評価関数

学習自体は上で説明した損失関数を使うのですが、損失関数が返す値は人間には分かりにくいという欠点があります。
そこで人間が評価しやすいように、損失関数とは別に「評価関数(metric function)」を損失関数と併用して学習結果を評価する場合があります。

損失関数と同じ様に評価関数にも色々な種類がありますが、今回は「正解率(accuracy)」を利用します。
今回の様に多クラス分類問題、かつラベルが one-hot ベクトル形式の場合は以下のソース 3 で示した関数によって計算できます。

ソース 3: 正解率(カテゴリカルデータ用)

def categorical_accuracy(predict,label):
    predict_amax = np.argmax(predict.numpy(),axis=1)
    label_amax = np.argmax(label.numpy(),axis=1)
    equal = np.equal(predict_amax, label_amax)
    return np.mean(equal)

※1 predict: 学習・検証・テストデータセットから求めた予測値
※2 label : 正しいラベル (one-hot ベクトル形式)

評価関数は学習に関係無いので @tf.function を付けずただの Python の関数として定義しています

GetTitle()

1. 学習データセットによるディープラーニングの実行