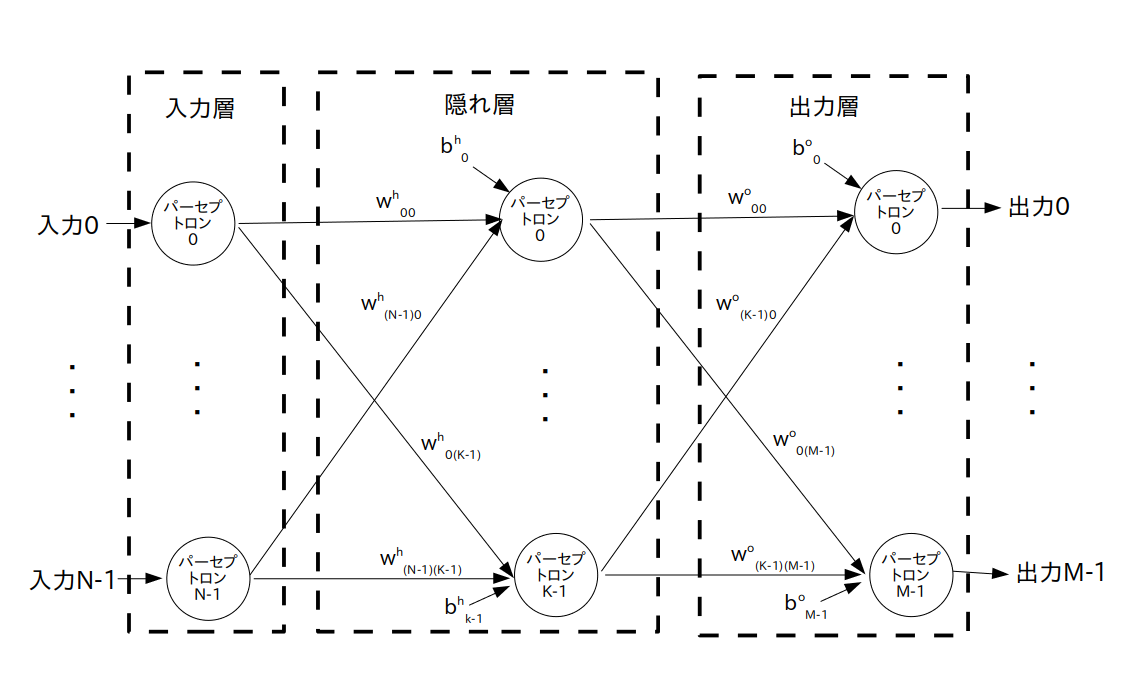
入力層(Input Layer)が N 個、隠れ層(Hidden Layer)が K 個、出力層(Output Layer)が M 個のパーセプトロンで出来ている
では早速 Keras を用いて MLP の構築と学習をしてみましょう。
今回も MLP として3層ニューラルネットワークを使います(図1)。
入力層(Input Layer)が N 個、隠れ層(Hidden Layer)が K 個、出力層(Output Layer)が M 個のパーセプトロンで出来ている

この3層ニューラルネットワークを Keras を用いて構築する例が次のソース 1 です。
生の TensorFlow を使った時と異なり、とてもシンプルに 3 層ニューラルネットワークを構築出来ます。
import tensorflow as tf
# パーセプトロンの数
N = 3 # 入力層の数
K = 5 # 隠れ層の数
M = 2 # 出力層の数
# 入力信号
data = tf.constant( [[1, 2, 3]], dtype=tf.float32 )
# 3層ニューラルネットワークの構築
model = tf.keras.Sequential()
model.add( tf.keras.Input(shape=(N,)))
model.add( tf.keras.layers.Dense(K, activation='tanh') )
model.add( tf.keras.layers.Dense(M, activation='softmax') )
# モデルの概要表示
model.summary()
# 出力 ※ 戻り値は numpy 配列
y = model.predict(data)
print('入力')
tf.print( data )
print('\n出力')
print( y )
では各行の意味について順を追って説明していきたいと思います。
まず最初の
import tensorflow as tf # パーセプトロンの数 N = 3 # 入力層の数 K = 5 # 隠れ層の数 M = 2 # 出力層の数 # 入力信号 data = tf.constant( [[1, 2, 3]], dtype=tf.float32 )
でパーセプトロンの数や入力信号を定義しています。
次の
# 3層ニューラルネットワークの構築 model = tf.keras.Sequential()
の行ではSequentialクラスのインスタンスである model を作成しています。
ニューラルネットワークの構造(モデル)として Sequential モデルを選ぶと add メソッドを使って各層を順々に積み重ねることが出来るようになります。
例えば次の
model.add( tf.keras.Input(shape=(N,)))
ではパーセプトロン数 N の入力層(Inputクラス)をモデルに追加しています。
また
model.add( tf.keras.layers.Dense(K, activation='tanh') )
の行では隠れ層としてパーセプトロン数 K 、活性化関数tanhの全結合層(Denseクラス)をモデルに追加しています。
そして最後に
model.add( tf.keras.layers.Dense(M, activation='softmax') )
の行では出力層としてパーセプトロン数 M 、活性化関数softmaxの全結合層(Denseクラス)をモデルに追加しています。
これで3層ニューラルネットワークモデルが出来たので、次の行の
model.summary()
でモデルの概要を表示します(図2)。
図2. リスト1で構築したモデルの概要 Model: "sequential_10" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_20 (Dense) (None, 5) 20 _________________________________________________________________ dense_21 (Dense) (None, 2) 12 ================================================================= Total params: 32 Trainable params: 32 Non-trainable params: 0
この図 2 に示したモデル概要を見ると、確かに K=5 の隠れ層と M=2 の出力層からなる3層ニューラルネットワークになっている事が分かります(上から下に向かって信号が流れます)。
なお Param の列にある数字(20と12)は各層のパラメータの個数、Total params の数字(32)はパラメータ数の合計です。
図1より
隠れ層のパラメータ数: 隠れ層の重みの数 = N*K 個、バイアスの数 = K 個なので、合計 N*K+K = 3*5+5 = 20 個
出力層のパラメータ数: 出力層の重みの数 = K*M 個、バイアスの数 = M 個なので、合計 K*M+M = 5*2+2 = 12 個
全体の合計: 20 + 12 = 32
なので確かに数字が合っています。
そして最後に
y = model.predict(data)
の様にして predict メソッドを使って入力信号 data に対する出力 y、つまり予測値を求めます。