ここでは FIR ローパスフィルタを設計したいと思います。

まずインパルス応答が時刻 $-\infty$ から $\infty$ まで存在する仮想のディジタルフィルタを考えます。
このフィルタは時刻 $0$ にインパルス信号を入力する前からインパルス応答が出力されているという不思議なフィルタなので現実には存在しません。
この様なフィルタを「非因果的なディジタルフィルタ」と呼びます。

この非因果的なディジタルフィルタのインパルス応答を Z 変換して伝達関数を求めます。

※ $\sum$ の範囲が $-\infty$ から $\infty$ まであるので両側 Z 変換になります。

非因果的なディジタルフィルタの伝達関数

インパルス応答が時刻 $-\infty$ から $\infty$ まであるディジタルフィルタのことを「非因果的なディジタルフィルタ」と呼び、その伝達関数は以下で表される。

\begin{align*} \textrm{H}(z) = \sum_{i=-\infty}^{\infty} \{ h[i] \cdot z^{-i} \} \end{align*}

さてこのフィルタが安定であると仮定し、伝達関数に $z = \textrm{e}^{j \cdot w \cdot \tau}$ を代入して周波数特性 $\textrm{H}(w)$ を求めます。
ここで $\tau$ [秒] はサンプリング間隔です。

非因果的なディジタルフィルタの周波数特性 \begin{align*} \textrm{H}(w) = \sum_{i = -\infty}^{\infty} \left \{ h[i] \cdot \textrm{e}^{\{ -j \cdot i \cdot w \cdot \tau \}} \right \} \end{align*}

この式は $h[i]$ の 離散時間フーリエ変換(DTFT)となっている事に注目して下さい。

次に $\textrm{H}(w)$ をフィルタの仕様に従って好きに設計し、$\textrm{H}(w)$ の逆離散時間フーリエ変換(IDTFT)によってインパルス応答 $h[i]$ を求めます。
ただし $\textrm{H}(w)$ は周期 $w_s$ [rad/秒] の周期的な複素関数にする必要があります。
さらに、少しトリッキーな話になりますが、計算を簡単にするために

「振幅特性 $|\textrm{H}(w)|$ は偶関数である」

「位相特性 $\angle \textrm{H}(w)$ は常に 0 である」

という仮定します(図1)。

図1： 周波数特性が偶関数かつ周期 $w_s$ [rad/秒] の実関数であると仮定する

　

当然ですがこの図 1 はただの例ですので、フィルタ仕様に従って自分で好きに振幅特性を決めても結構です。

さて $\textrm{H}(w)$ は実関数でかつ偶関数であると仮定したのでインパルス応答 $h[i]$ も偶関数となり以下の式で求められます。

※ この式の導出方法はこちら

非因果的なディジタルフィルタのインパルス応答 \begin{align*} h[i] = \frac{2}{w_s} \int_{0}^{w_s/2} \left \{ \textrm{H}(w) \cdot \cos ( i \cdot w \cdot \tau ) \right \} \textrm{dw} \end{align*}


準備が終わりましたので、早速ローパスフィルタを設計してみましょう。

まず $\textrm{H}(w)$ としてカットオフ角周波数を $w_c$ [rad/秒] とした理想的なローパス特性を設定します(図2)。

図2： 理想的なローパス特性

　

$w_c$ ・・・ カットオフ角周波数、$w_c \leq w_s/2$、単位は[rad/秒]

図2の $\textrm{H}(w)$ に対するインパルス応答は

\begin{align*} h[i] &= \frac{2}{w_s} \int_{0}^{w_s/2} \left \{ \textrm{H}(w) \cdot \cos (i \cdot w \cdot \tau ) \right \} \textrm{dw} \\ &= \frac{2}{w_s} \int_{0}^{w_c} \left \{ 1 \cdot \cos ( i \cdot w \cdot \tau ) \right \} \textrm{dw} \\ &= \frac{2}{w_s} \cdot \frac{1}{ i \cdot \tau} \cdot \sin ( i \cdot w_c \cdot \tau ) \\ (\tau = 2\pi/w_s \ \text{より}) &= \frac{1}{\pi \cdot i } \cdot \sin \left [ \pi \cdot i \cdot \frac{w_c}{(w_s/2)} \right ] \\ (\alpha = \frac{w_c}{(w_s/2)} \ \text{とおいて}) &= \frac{\sin ( \pi \cdot i \cdot \alpha )}{\pi \cdot i } \end{align*}

となります。
なお $i=0$ の時は

\[ \lim_{x\rightarrow 0} \frac{\sin(x)}{x} = 1 \]

の公式に $x = \pi \cdot i \cdot \alpha$ を代入することで

\[ h[0] = \alpha \]

となります。
また $f_s$ [Hz] をサンプリング周波数、$f_c$ [Hz] をカットオフ周波数とすると

\begin{align*} \alpha &= \frac{w_c}{(w_s/2)} \\ &= \frac{ 2\pi \cdot f_c }{ ( 2\pi\cdot f_s /2) }\\ &= \frac{f_c}{(f_s/2)} \end{align*}

と変形できます。
つまり $\alpha$ はカットオフ周波数 $f_c$ がナイキスト角周波数 $f_s/2$ の時に $\alpha = 1$ になるように正規化されていることになります。
そのため $\alpha$ のことを「正規化カットオフ周波数」と言います。

以上をまとめると次のようになります。

非因果的な理想ローパスフィルタのインパルス応答

$w_c$ [rad/秒] ・・・ カットオフ角周波数

$w_s$ [rad/秒] ・・・サンプリング角周波数

$f_c$ [Hz] ・・・カットオフ周波数

$f_s$ [Hz] ・・・サンプリング周波数

とする。
また $\alpha$ を正規化カットオフ周波数

\begin{align*} \alpha = \frac{w_c}{(w_s/2)} = \frac{f_c}{(f_s/2)} \end{align*}

とする。

すると非因果的な理想ローパスフィルタのインパルス応答は次の式で表される。

\begin{align*} h[0] = \alpha \end{align*} \begin{align*} h[-i] = h[i] = \frac{\sin ( \pi \cdot i \cdot \alpha )}{(\pi \cdot i) }\ ,\ (i = 1, 2, \cdots) \end{align*}

ただしこのままではインパルス応答が無限個存在することになってしまうので、インパルス応答を途中で打ち切って無理やり FIR フィルタにします。

そのためにまず FIRフィルタ長として適当な正整数 $\textrm{L}$ を決め(ただし $\textrm{L}$ は奇数とします)、次に正整数 $\textrm{C} = (\textrm{L}-1)/2$ を定義し、$h[-\textrm{C}]$ から $h[\textrm{C}]$ までの $\textrm{L}$ 個のインパルス応答だけ取り出します(図3)。

図3： インパルス応答を $\textrm{L}$ 個だけ取り出して無理やり FIR フィルタにする

$\alpha = 0.5$、$\textrm{L} = 13$、$\textrm{C}=6$ の例


[ビフォー]

→　[アフター]

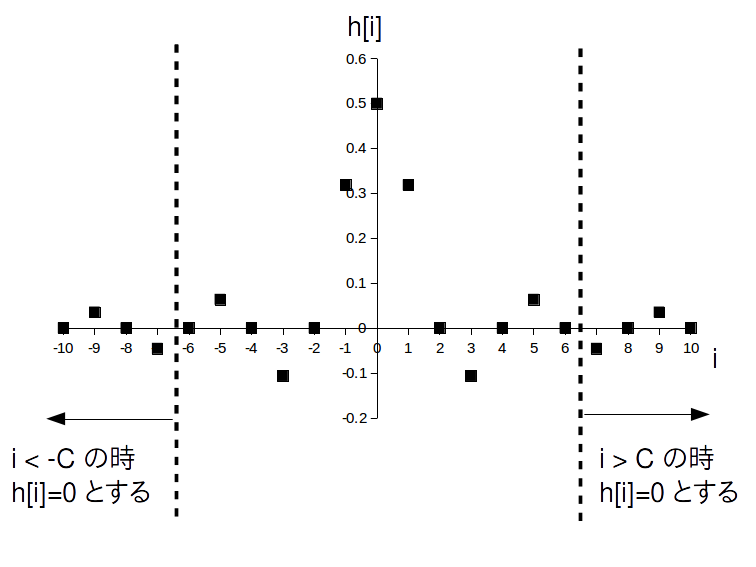
もちろん無理やりFIRフィルタにしたので周波数特性も変化します。
具体的に計算すると周波数特性は

\begin{align*} \textrm{H}(w) &= \sum_{i = -\textrm{C}}^{\textrm{C}} \left \{ h[i] \cdot \textrm{e}^{\{ -j \cdot i \cdot w \cdot \tau \}} \right \} \\ & = h[0] + \sum_{i = -1}^{-\textrm{C}} \left \{ h[i] \cdot \textrm{e}^{\{ -j \cdot i \cdot w \cdot \tau \}} \right \} + \sum_{i = 1}^{\textrm{C}} \left \{ h[i] \cdot \textrm{e}^{\{ -j \cdot i \cdot w \cdot \tau \}} \right \} \\ (h[i] = h[-i] \ \textrm{なので}) & = h[0] + \sum_{i = 1}^{\textrm{C}} \left [ h[i] \cdot \left \{ \textrm{e}^{\{ j \cdot i \cdot w \cdot \tau \}} + \textrm{e}^{\{ -j \cdot i \cdot w \cdot \tau \}} \right \} \right ] \\ \end{align*}

最後の式にオイラー公式を適用すると周波数特性は次のように求まります。

非因果的な FIR ローパスフィルタの周波数特性

　

\begin{align*} \textrm{H}(w) = h[0] + \sum_{i = 1}^{\textrm{C}} \left \{ 2 \cdot h[i] \cdot \cos (i\cdot w \cdot \tau ) \right \} \end{align*}

ここで

\begin{align*} h[0] = \alpha \end{align*} \begin{align*} h[i] = \frac{\sin ( \pi \cdot i \cdot \alpha )}{(\pi \cdot i) }\ ,\ (i = 1, \cdots, \textrm{C} ) \end{align*}

周波数特性のグラフ例を図4に示します。
このように、無限インパルス応答を途中で打ち切った影響で周波数特性が波打っているような形に変化します(図2と見比べてみましょう)。
この波打ち現象の事を「ギブズ現象」と言います。

このギブス現象を軽減させるため、普通は FIR フィルタを設計する際にハミング窓などの「窓関数」がインパルス応答にかけられます。

※ 今回のアクティビティでは窓関数を扱いませんので必要になった時に自分で調べて下さい。

図4： 非因果的な FIR ローパスフィルタの周波数特性の例

$w_s = 2\pi$、$w_c = \pi/2$、$\alpha = 0.5$、$\textrm{L} = 13$、$\textrm{C}=6$ の例

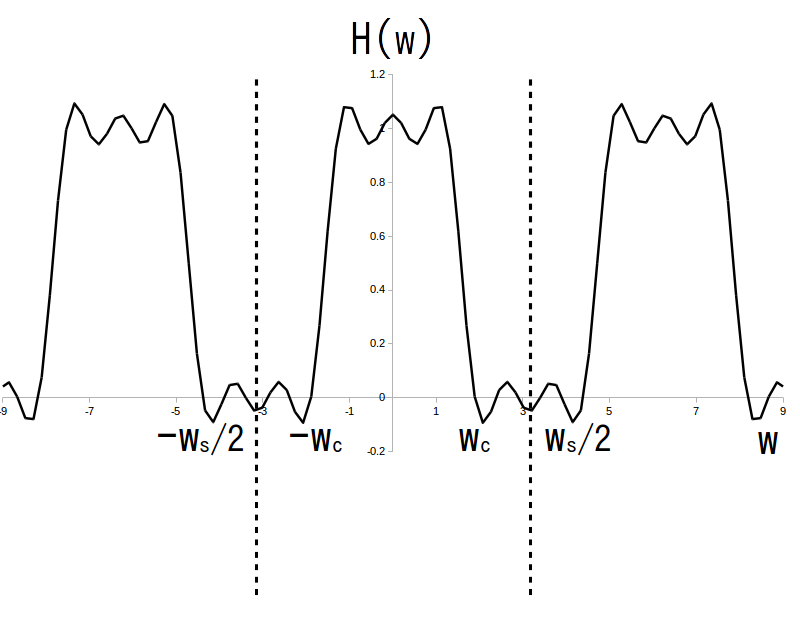
次に因果性を満たすフィルタになるようにインパルス応答を変化させます。

※ 「因果性を満たすフィルタ」とはインパルス信号を入力してからインパルス応答が出てくる普通のディジタルフィルタのことです。

と言っても単に時刻 $\textrm{C}$ だけインパルス応答を遅延させるだけなので、結局 FIR ローパスフィルタのインパルス応答は次のようになります。

FIR ローパスフィルタのインパルス応答

$w_c$ [rad/秒] ・・・ カットオフ角周波数

$w_s$ [rad/秒] ・・・サンプリング角周波数

$f_c$ [Hz] ・・・カットオフ周波数

$f_s$ [Hz] ・・・サンプリング周波数

とする。
また $\alpha$ を正規化カットオフ周波数

\begin{align*} \alpha = \frac{w_c}{(w_s/2)} = \frac{f_c}{(f_s/2)} \end{align*}

とする。
さらに FIRフィルタ長として適当な正整数 $\textrm{L}$ を決め(ただし $\textrm{L}$ は奇数とする)、正整数 $\textrm{C} = (\textrm{L}-1)/2$ を定義する。

この時、FIR ローパスフィルタのインパルス応答は次の式で表される。

\begin{align*} h[\textrm{C}] = \alpha \end{align*} \begin{align*} h[\textrm{C}-i] = h[\textrm{C}+i] = \frac{\sin ( \pi \cdot i \cdot \alpha )}{(\pi \cdot i) }\ ,\ (i = 1, 2, \cdots, \textrm{C} ) \end{align*}

伝達関数は次のようになります。

FIR ローパスフィルタの伝達関数

$h[i]$ を上で計算した FIR ローパスフィルタのインパルス応答とした時

\begin{align*} \textrm{H}(z) = \sum_{i=0}^{\textrm{L}-1} \{ h[i] \cdot z^{-i} \} \end{align*}

なおインパルス応答を時刻 $\textrm{C}$ だけ遅延させた影響で位相特性が変化しますが、元の非因果的なFIRフィルタにC 時刻遅延素子 $z^{-\textrm{C}}$ を直列結合 しただけなので、FIRローパスフィルタの周波数特性は次のようになります。

FIR ローパスフィルタの周波数特性

$h[i]$ を上で計算した FIR ローパスフィルタのインパルス応答とした時

\begin{align*} \textrm{H}(w) = \left ( h[\textrm{C}] + \sum_{i = 1}^{\textrm{C}} \left \{ 2 \cdot h[\textrm{C}+i] \cdot \cos (i\cdot w \cdot \tau ) \right \} \right ) \cdot \textrm{e}^{ -j \cdot w \cdot \textrm{C} \cdot \tau } \end{align*}

つまりFIRローパスフィルタの位相特性は

\begin{align*} \angle \textrm{H}(w) = - w \cdot \textrm{C} \cdot \tau \end{align*}

となるのですが、これは $w$ [rad/秒] に対して傾き $-\textrm{C} \cdot \tau$の直線を表していますので、FIRローパスフィルタの位相特性の事を「直線位相特性」と呼びます。
逆に、FIRローパスフィルタは直線位相特性を持っているので、どんな角周波数のサイン波を入力しても必ず $\textrm{C}$ 時刻だけ遅れて出てくるとも言えます。

ちなみにこの周波数特性の式は $h[i]$が $\textrm{C}$ を中心に偶関数となっていればどんな $h[i]$ に対しても成り立ちます。
例えば前ページで扱った移動平均フィルタの場合は $h[i] = 1/\textrm{L}$ でしたので、これを周波数特性の式に代入することで移動平均フィルタの周波数特性が求まります。