演習1-1 (個人): 伝達関数
\[ \textrm{H}(z) = a + b \cdot z^{-n} \]を持つフィルタ、つまりディレイフィルタ(delay filter)を作って自分の声にディレイ効果をかけてみましょう。
マイクを PC の端子に繋ぎます。
マイクの設定を開いて音量調整をします。
レコーダーを開きます。
「3 秒以上」録音し、ダウンロードフォルダに音声ファイル( out.wav ) をダウンロードします。
out.wav を試しに再生し、もし音が小さい場合は録音し直します。
out.wav を演習フォルダに移動して「 DF_1_1.wav 」に名前を変更します。
Jupyter Notebook を起動します。
新規ノートブックを作って「DF_1_1」に名前を変更します。
一番上のセルにテンプレートの内容をコピーします。
穴埋め問題を解いて実行するとフィルタリング前後のスペクトログラムと「 DF_1_1_out.wav 」という Wave形式音声ファイルが出来ます。
DF_1_1_out.wav を再生して自分の声にディレイ効果がかかっている事を確認して下さい。
パラメータ(a,b,delay)を色々変えると効果が色々変化することを確認して下さい。
指定場所に「ソースコード」、「フィルタリング前のスペクトログラム」と「フィルタリング後のスペクトログラム」を貼り付けて下さい。
演習1-2 (個人): 伝達関数
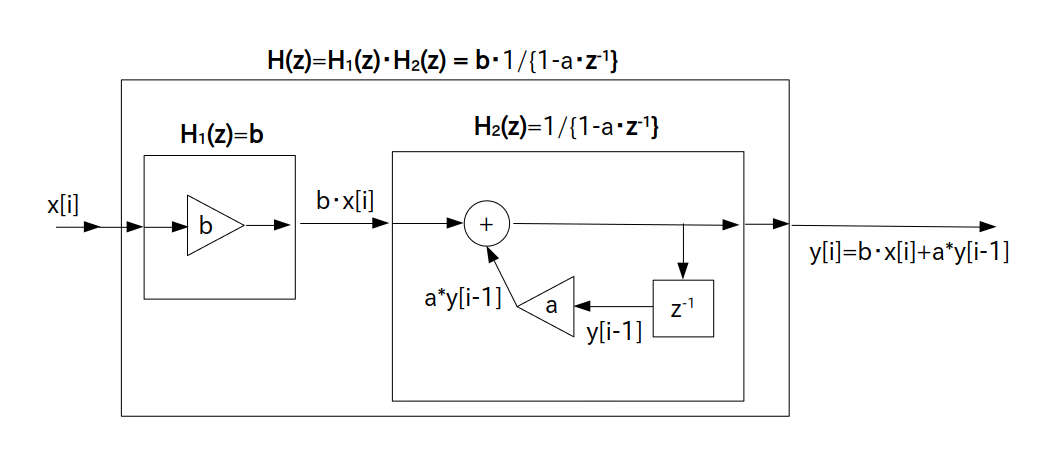
\begin{align*} \textrm{H}(z) = b \cdot \frac{1}{1- a \cdot z^{-1}} \end{align*}を持つフィルタを作ってみましょう。
なお $a = 0.87$、$b=0.14$ とします。
(ヒント) $\textrm{H}_1(z)$ を乗算器
\begin{align*} \textrm{H}_1(z) = b \end{align*}$\textrm{H}_2(z)$ をフィードバック機構をもつフィルタ
\begin{align*} \textrm{H}_2(z) = \frac{1}{1- a \cdot z^{-1}} \end{align*}としたとき、$\textrm{H}(z)$ は $\textrm{H}_1(z)$ と $\textrm{H}_2(z)$ を直列結合したフィルタであるので、ブロック図は以下のようになる。

音声は引き続き「 DF_1_1.wav 」を使用します。
Jupyter Notebook を起動します。
新規ノートブックを作って「DF_1_2」に名前を変更します。
一番上のセルにテンプレートの内容をコピーします。
穴埋め問題を解いて実行するとフィルタリング前後のスペクトログラムと「 DF_1_2_out.wav 」という Wave形式音声ファイルが出来ます。
DF_1_2_out.wav を再生してどの様な効果がかかっているか確認して下さい。
指定場所に「ディジタル線形フィルタの計算部のソースコード」、「フィルタリング前のスペクトログラム」と「フィルタリング後のスペクトログラム」を貼り付けて下さい。